Question 11.3: A viewing platform in a wild-animal park (Fig. 11-21a) is su...
A viewing platform in a wild-animal park (Fig. 11-21a) is supported by a row of aluminum pipe columns having a length L =10 ft 8 in. and an outer diameter d = 4 in. The bases of the columns are set in concrete footings, and the tops of the columns are supported laterally by the platform. The columns are being designed to support compressive loads where P = 22.5kips.
Determine the minimum required thickness t of the columns (Fig. 11-21b) if a factor of safety n = 3 is required with respect to Euler buckling. (For the aluminum, use 10,400 ksi for the modulus of elasticity and use 70 ksi for the proportional limit.)

Learn more on how we answer questions.
Use a four-step problem-solving approach. Combine steps as needed for an efficient solution.
1, 2. Conceptualize, Categorize:
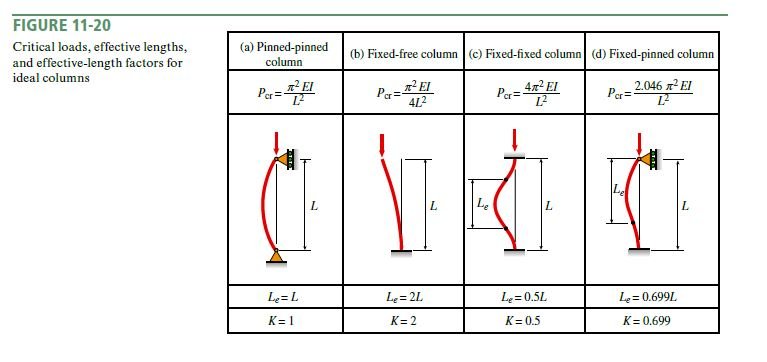
Critical load: Because of the manner in which the columns are constructed, each column is modeled as a fixed-pinned column (see Fig. 11-20d). Therefore, the critical load is
P_{ cr }=\frac{2.046 \pi^{2} E I}{L^{2}} (a)
in which I is the moment of inertia of the tubular cross section:
I=\frac{\pi}{64}\left[d^{4}-(d-2 t)^{4}\right] (b)
Substitute d = 4 in. to get
I=\frac{\pi}{64}\left[(4 \text { in. })^{4}-(4 \text { in. }-2 t)^{4}\right] (c)
in which t is expressed in inches.
3. Analyze:
Required thickness of the columns: Since the load per column is 22.5 kips and the factor of safety is 3, each column must be designed for the critical load:
Substitute this value for P_{cr} in Eq. (a), and also replace I with its expression from Eq. (c) to obtain
67.5 kips =\frac{2.046 \pi^{2}(10,400 ksi )}{(128 in .)^{2}}\left[\frac{\pi}{64}\left[(4 in. )^{4}-(4 in. -2 t)^{4}\right]\right]Note that all terms in this equation are expressed in units of kips and inches.
Solve the previous equation to find that the minimum required thickness of the column to meet the specified conditions is
t_{\min }=0.254 in.4. Finalize:
Supplementary calculations: Knowing the diameter and thickness of the column, now calculate its moment of inertia, cross-sectional area, and radius of gyration. Using the minimum thickness of 0.254 in. gives
A=\frac{\pi}{4}\left[d^{2}-(d-2 t)^{2}\right]=2.989 in ^{2} \quad r=\sqrt{\frac{I}{A}}=1.327 in.
The slenderness ratio L/r of the column is approximately 96.5, which is in the customary range for slender columns, and the diameter-to-thickness ratio d/t is approximately 16, which should be adequate to prevent local buckling of the walls of the column.
The critical stress in the column must be less than the proportional limit of the aluminum if the formula for the critical load of Eq. (a) is to be valid. The critical stress is
\sigma_{ cr }=\frac{P_{ cr }}{A}=\frac{67.5 kips }{2.989 in ^{2}}=22.6 ksiwhich is less than the proportional limit (70 ksi). Therefore, the calculation for the critical load using the Euler buckling theory is satisfactory.