Question 15.9: Find the vibration frequencies of a linear three-atom symmet...
Find the vibration frequencies of a linear three-atom symmetric molecule ABA. We assume that the potential energy of the molecule depends only on the distances AB and BA and the angle ABA. Write the Lagrangian of the molecule in appropriate coordinates (normal coordinates) where the Lagrangian has the form
L =\sum\limits_{α}{\frac{m_{α}}{2} ( \dot{Θ}^{2}_{α}−ω^{2}_{α} Θ^{2}_{α})}.The ω_{α} are the desired vibration frequencies of the normal modes. If one cannot find the normal coordinates of the system, one can proceed as follows: If a system has s degrees of freedom and does not vibrate, then the Lagrangian generally reads
L = \frac{1}{2} \sum\limits_{i,k}{(m_{ik} \dot{x}_{i} \dot{x}_{k} −k_{ik}x_{i}x_{k})}.The eigenfrequencies of the system are then determined by the so-called characteristic equation
det|k_{ik} −ω^{2}m_{ik}| = 0.
Learn more on how we answer questions.
We describe the geometry of the molecule in the x,y-plane. Let the displacement of the atom α from the rest position r_{α0} be denoted by x_{α} = (x_{α}, y_{α}), i.e., r_{α} = r_{α0} +x_{α}. The forces that keep the atoms together are assumed to be to first order linear in the displacement from the rest position, i.e.,
L = \frac{m_{A}}{2} (\dot{x}^{2}_{1} + \dot{x}^{2}_{3} )+ \frac{m_{B}}{2} \dot{x}^{2}_{2} − \frac{KL}{2}[(x_{1} − x_{2})^{2} + (x_{3} −x_{2})^{2}],if we consider longitudinal vibrations. For these modes the conservation of the center of gravity can be written as follows:
m_{A}(x_{1} +x_{3})m_{B}x_{2} = 0, \left[ \sum\limits_{α}{m_{α}r_{α}} =\sum\limits_{α}{m_{α}r_{αo}}\right],and we can eliminate x_{2} from L:
L = \frac{m_{A}}{2} (\dot{x}^{2}_{1} + \dot{x}^{2}_{3} )+ \frac{m^{2}_{A}}{2m_{B}}(\dot{x}_{1} + \dot{x}_{3})^{2}-\frac{K_L}{2} \left[ x^{2}_{1}+x^{2}_{3}+2 \frac{m_{A}}{m_{B}}(x_{1} +x_{3})^{2} +\frac{2m^{2}_{A}}{m^{2}_{B}}(x_{1} +x_{3})^{2}\right].
Hence, only two normal coordinates for the longitudinal motion can exist, because of the conservation of the center of gravity.
Let Θ_{1} = x_{1} + x_{3},Θ_{2} = x_{1} −x_{3}. L can then be written as
L = \frac{m_{A}}{4}\dot{Θ}^{2}_{2} + \frac{m_{A}μ}{4m_{B}} \dot{Θ}^{2}_{1} − \frac{KL}{4} Θ^{2}_{2} − \frac{K_{L}μ}{4m^{2}_{B}} Θ^{2}_{1}, μ≡ 2m_{A} +m_{B},i.e., Θ_{1} and Θ_{2} are the two normal coordinates of the longitudinal vibration (μ represents the total mass of the molecule).
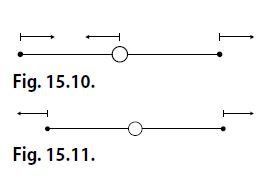
(a) For x_{1}= x_{3}, Θ_{2} vanishes; i.e., Θ_{1} describes antisymmetric longitudinal vibrations (Fig. 15.10).
(b) For x_{1} =−x_{3}, Θ_{1} vanishes; i.e., Θ_{2} describes symmetric longitudinal vibrations (Fig. 15.11).
A comparison of kinetic and potential energy yields the normal frequencies
ω_{a} =\sqrt{\frac{K_{L}μ}{m_{A}m_{B}}}, antisymmetric vibration,
ω_{s} =\sqrt{\frac{K_{L}}{m_{A}}}, symmetric vibration.
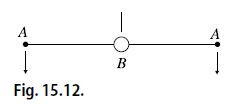
For transverse vibrations (see Fig. 15.12) of the form in Fig. 15.13, we set
L = \frac{m_{A}}{2} (\dot{y}^{2}_{1}+ \dot{y}^{2}_{3} )+ \frac{m_{B}}{2} \dot{y}^{2}_{2} − \frac{K_{T}}{2} (lδ)^{2},where δ is the deviation of the angle ∢ (ABA) from π. For small values of δ, we can set
δ =\left(\frac{π}{2} − α_{1}\right)+\left(\frac{π}{2} − α_{2}\right)=sin \left(\frac{π}{2} − α_{1}\right)+sin \left(\frac{π}{2} − α_{2}\right)
= cos α_{1} + cos α_{2}
= \frac{y_{2} −y_{1}}{l} + \frac{y_{2} −y_{3}}{l}.
We utilize the conservation of the center of gravity and angular momentum conservation to eliminate y_{2} and y_{3} from L.
m_{A}(y_{1} + y_{3})+ m_{B}y_{2} = 0 (conservation of the center of gravity).
To exclude rotation of the molecule, the total angular momentum must vanish:
D =\sum\limits_{α}{m_{α}[r_{α} ×v_{α}]} \simeq \sum\limits_{α}{m_{α}[r_{α0} × \dot{x_{α}}]} = \frac{d}{dt}\sum\limits_{α}{m_{α}[\dot{r}_{α0} ×x_{α}]},which can be achieved by
\sum\limits_{α}{m_{α}[r_{α0} ×x_{α}]} = 0.For our case, it thus follows that y_{1} = y_{3}.Then we get
(l \dot{δ})^{2} =\frac{4μ^{2}\dot{y}^{2}_{1}}{m^{2}_{β}} and L = \frac{m_{A}m_{B}}{4μ}l^{2} \dot{δ}^{2} − \frac{K_{T} l^{2}}{2} δ^{2}.
We thus obtain the eigenfrequency of the transverse vibration:
ω_{T} =\sqrt{\frac{2K_{T} μ}{m_{A}m_{B}}}.