Question 18.5: This is an example with a constraint. A chain of constant de...
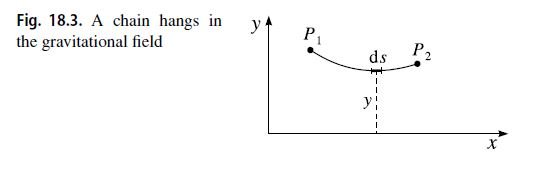
This is an example with a constraint. A chain of constant density σ (mass per unit length: σ = dm/ds) and length l hangs in the gravitational field between two points P_{1}(x_{1}, y_{1}) and P_{2}(x_{2}, y_{2}).We look for the form of the curve, assuming that the potential energy of the chain takes a minimum.
Learn more on how we answer questions.
The potential energy of a chain element is
dV = gσy ds.The total potential energy is then
V = gσ \int\limits_{x_{1}}^{x_{2}}{y ds},where the line element is given by
ds =\sqrt{1 +y^{′2}} dx, y^{′} = \frac{dy}{dx}.The constraint of given length l is represented by
0 =\int\limits_{x_{1}}^{x_{2}}{ds − l} =\int\limits_{x_{1}}^{x_{2}}{\sqrt{1 +y^{′2}} dx −l}.With the Lagrange multiplier λ, the variational problem reads
gσ δ \int\limits_{x_{1}}^{x_{2}}{y \sqrt{1 +y^{′2}} dx}−λδ \left( \int\limits_{x_{1}}^{x_{2}}{\sqrt{1 +y^{′2}} dx}− l\right)= 0.Since δl = 0, we can introduce the function
F(y,y^{′}) = (y −μ) \sqrt{1 +y^{′2}}in the Euler equation (18.32), where we chose μ = λ/gσ. From
\frac{∂F}{∂y} − \frac{d}{dx} \frac{∂F}{∂y^{′}}= 0,it follows that
(y −μ)y^{″} −y^{′2} −1 = 0.We rewrite the last equation. With
y^{″} =\frac{dy^{′}}{dx} = \frac{dy^{′}}{dy} \frac{dy}{dx} = y^{′} \frac{dy^{′}}{dy},we obtain
(y −μ)y^{′} \frac{ dy^{′}}{dy} = y^{′2} +1, \frac{dy}{y −μ}= \frac{y^{′}dy^{′}}{1 +y^{′2}} .Integration yields
ln(y −μ)+lnC_{1} = \frac{1}{2} ln(1 +y^{′2})or
C_{1}(y −μ) =\sqrt{1 +y^{′2}}.From this, we get
\int{\frac{dy}{\sqrt{C^{2}_{1} (y −μ)^{2} −1}}}= \int{dx}.To integrate the left side, we substitute cosh ν = C_{1}(y − ν), since cosh^{2} ν − 1 = sinh^{2} ν. Then
dy = \frac{1}{C_{1}}sinh νdν,and therefore,
\frac{1}{C_{1}} \int{dν} =\int{dx}.Integration yields
ν = C_{1}(x +C_{2})or
y = \frac{1}{C_{1}} cosh(C_{1}(x +C_{2})) +μ.Thus, the solution is the catenary. The constants give the coordinates of the lowest point (x_{0}, y_{0}) = (−C_{2}, (1/C_{1})+μ). They are determined by the given length l of the chain and by the suspension points P_{1} and P_{2}.