Question 10.2.10: Transforming a Letter The capital letter L in Figure 2 is de...
Transforming a Letter
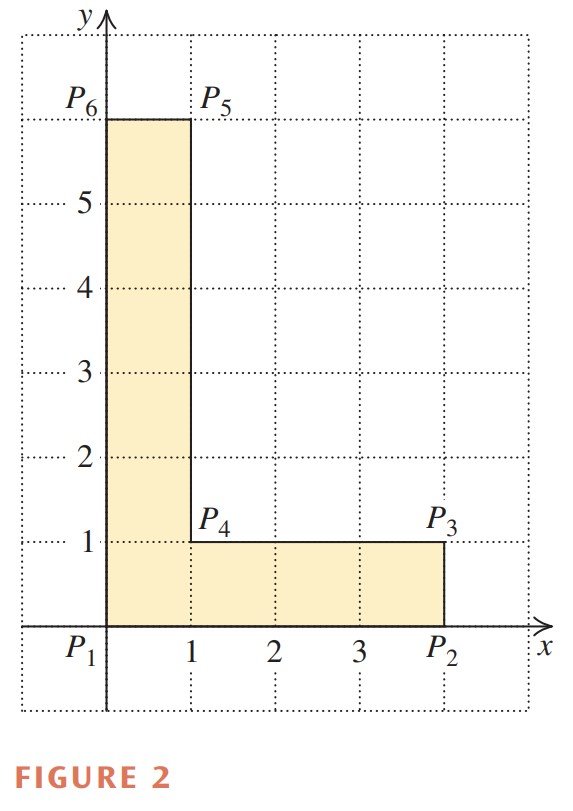
The capital letter L in Figure 2 is determined by six points (or vertices) P_{1} through P_{6} . The coordinates of the six points can be stored in a data matrix D. We draw line segments connecting these vertices in order.
\begin{array}{llllll}&\, P_{1} \enspace P_{2} \enspace P_{3} \enspace P_{4} \enspace P_{5} \enspace P_{6}\\ \begin {array}{r} x \text {-coordinate } \\ y \text {-coordinate } \end {array} & \left[\begin{array}{llllll}0 & 4 & 4 & 1 & 1 & 0 \\0 & 0 & 1 & 1 & 6 & 6\end{array}\right] =D \end{array}
If A=\left[\begin{array}{ll}1 & 0.25 \\0 & 1\end{array}\right], compute AD and graph the figure it represents.
The columns of the product matrix AD represent the transformed vertices of the letter L.
A D=\left[\begin{array}{ll}1 & 0.25 \\0 & 1\end{array}\right]\left[\begin{array}{llllll}0 & 4 & 4 & 1 & 1 & 0 \\0 & 0 & 1 & 1 & 6 & 6\end{array}\right]
=\left[\begin{array}{llllll}1 \cdot 0+0.25 \cdot 0 & 1 \cdot 4+0.25 \cdot 0 & 1 \cdot 4+0.25 \cdot 1 & 1 \cdot 1+0.25 \cdot 1 & 1 \cdot 1+0.25 \cdot 6 & 1 \cdot 0+0.25 \cdot 6 \\0 \cdot 0+1 \cdot 0 & 0 \cdot 4+1 \cdot 0 & 0 \cdot 4+1 \cdot 1 & 0 \cdot 1+1 \cdot 1 & 0 \cdot 1+1 \cdot 6 & 0 \cdot 0+1 \cdot 6\end{array}\right]
\begin{array}{lllll}&\enspace P_{1}^{\prime} \quad P_{2}^{\prime}\quad P_{3}^{\prime}\quad P_{4}^{\prime}\quad \, P_{5}^{\prime}\quad \, P_{6}^{\prime}\\ =&\left[\begin{array}{llllll}0 & 4 & 4.25 & 1.25 & 2.5 & 1.5 \\0 & 0 & 1 & 1 & 6 & 6\end{array}\right]\end{array}
Figure 3 shows the transformed vertices and the transformed figure formed by these vertices.
