Question 11.2: For the geometry in Example 11.1, determine the energy trans...
For the geometry in Example 11.1, determine the energy transfer from wall 1 to wall 2 by heat conduction combined with absorption and scattering in the optically thin limit.
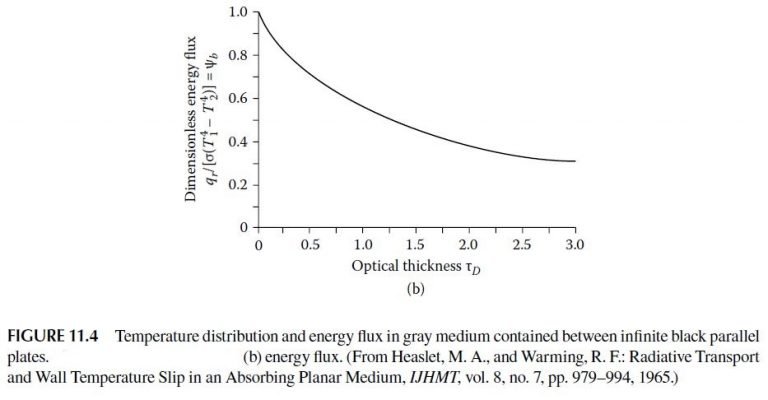
From Figure 11.4b, as τ_D →0, ψ_b , →1, so Equation 11.64
\frac{q_r}{\sigma (T_1^4-T_2^4)}=\frac{\psi _b}{1+\psi _b(1/\epsilon _1+1/\epsilon _2-2)} (11.64)
reduces to {q}={\sigma (T_1^4-T_2^4)}/(1/\epsilon _1+1/\epsilon _2-1), which is the same as the result without a radiating medium between the walls. Equation 11.61
\frac{T_1^4-T^4(\tau =0)}{T_1^4-T_2^4} \mid_{\tau _{D\longrightarrow 0}} =\frac{1}{2} (11.61)
shows that, in the optically thin limit, the radiative flux does not produce a temperature gradient in the medium and hence does not influence heat conduction. Ordinary heat conduction can thus be added to the radiation to give the combined flux in the optically thin limit,
q=\frac{k(T_1-T_2)}{D}+\frac{\sigma (T_1^4-T_2^4)\psi _b}{1+1/\epsilon _1+1/\epsilon _2-1} (11.67)
