Question 3.5: For the circuit in Fig. 3.18, find the branch currents I1, I...
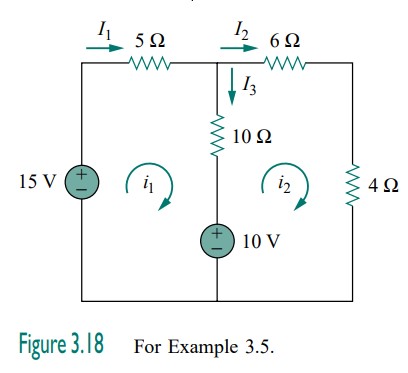
For the circuit in Fig. 3.18, find the branch currents I_{1}, I_{2}, \text { and } I_{3} using mesh analysis.
Learn more on how we answer questions.
We first obtain the mesh currents using KVL. For mesh 1,
-15+5 i_{1}+10\left(i_{1}-i_{2}\right)+10=0
or
3 i_{1}-2 i_{2}=1 (3.5.1)
For mesh 2,
6 i_{2}+4 i_{2}+10\left(i_{2}-i_{1}\right)-10=0
or
i_{1}=2 i_{2}-1 (3.5.2)
METHOD 1 Using the substitution method, we substitute Eq. (3.5.2) into Eq. (3.5.1), and write
6 i_{2}-3-2 i_{2}=1 \quad \Longrightarrow \quad i_{2}=1 A
From Eq. (3.5.2), i_{1}=2 i_{2}-1=2-1=1 A. Thus,
I_{1}=i_{1}=1 A , \quad I_{2}=i_{2}=1 A , \quad I_{3}=i_{1}-i_{2}=0
METHOD 2 To use Cramer’s rule, we cast Eqs. (3.5.1) and (3.5.2) in matrix form as
\left[\begin{array}{rr}3 & -2 \\-1 & 2\end{array}\right]\left[\begin{array}{l}i_{1} \\i_{2}\end{array}\right]=\left[\begin{array}{l}1 \\1\end{array}\right]
We obtain the determinants
\Delta=\left|\begin{array}{rr}3 & -2 \\-1 & 2\end{array}\right|=6-2=4
\Delta_{1}=\left|\begin{array}{rr}1 & -2 \\1 & 2\end{array}\right|=2+2=4, \quad \Delta_{2}=\left|\begin{array}{rr}3 & 1 \\-1 & 1\end{array}\right|=3+1=4
Thus,
i_{1}=\frac{\Delta_{1}}{\Delta}=1 A , \quad i_{2}=\frac{\Delta_{2}}{\Delta}=1 A
as before.