Question 3.6: Use mesh analysis to find the current io in the circuit in F...
Use mesh analysis to find the current i_{o} in the circuit in Fig. 3.20.

Learn more on how we answer questions.
We apply KVL to the three meshes in turn. For mesh 1,
-24+10\left(i_{1}-i_{2}\right)+12\left(i_{1}-i_{3}\right)=0
or
11 i_{1}-5 i_{2}-6 i_{3}=12 (3.6.1)
For mesh 2,
24 i_{2}+4\left(i_{2}-i_{3}\right)+10\left(i_{2}-i_{1}\right)=0
or
-5 i_{1}+19 i_{2}-2 i_{3}=0 (3.6.2)
For mesh 3,
4 i_{o}+12\left(i_{3}-i_{1}\right)+4\left(i_{3}-i_{2}\right)=0
But at node A, i_{o}=i_{1}-i_{2} , so that
4\left(i_{1}-i_{2}\right)+12\left(i_{3}-i_{1}\right)+4\left(i_{3}-i_{2}\right)=0
or
-i_{1}-i_{2}+2 i_{3}=0 (3.6.3)
In matrix form, Eqs. (3.6.1) to (3.6.3) become
\left[\begin{array}{rrr}11 & -5 & -6 \\-5 & 19 & -2 \\-1 & -1 & 2\end{array}\right]\left[\begin{array}{l}i_{1} \\i_{2} \\i_{3}\end{array}\right]=\left[\begin{array}{r}12 \\0 \\0\end{array}\right]
We obtain the determinants as
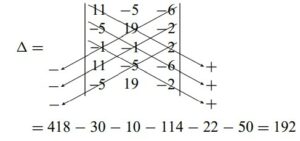



We calculate the mesh currents using Cramer’s rule as
\begin{gathered}i_{1}=\frac{\Delta_{1}}{\Delta}=\frac{432}{192}=2.25 A , \quad i_{2}=\frac{\Delta_{2}}{\Delta}=\frac{144}{192}=0.75 A \\i_{3}=\frac{\Delta_{3}}{\Delta}=\frac{288}{192}=1.5 A\end{gathered}
Thus, i_{o}=i_{1}-i_{2}=1.5 A.