Question 17.9: Your company is looking at purchasing a new front-end loader...
Your company is looking at purchasing a new front-end loader and has narrowed the choice down to four loaders. The purchase price, annual profit, and salvage value at the end of five years for each of the loaders is found in Table 17-5 . Which front-end loader should your company purchase based on the incremental net present values using a MARR of 20% and a useful life of five years?
Learn more on how we answer questions.
The first step is to rank the alternative in order of initial cost (purchase price). The loaders are compared in the following order: Loader A, Loader C, Loader B, and Loader D. Because Loader A has the lowest initial cost, it is designated the current best alternative.
Next, compare Loader A to Loader C. The difference in the purchase price is $10,000 ($120,000 – $110,000). The difference in annual profit is $3,000 ($40,000 – $37,000). The difference in salvage value is $2,000 ($12,000 – $10,000). The difference in the cash flows for these two alternatives is shown in Figure 17-7 .
The present value of the difference in annual profits is determined by using Eq. (15-9) as follows:
P=A\left[\frac{(1+i)^{n}-1}{i(1+i)^{n}}\right] (15-9)
P_{ AP }=\$ 3,000\left[\frac{(1+0.20)^{5}-1}{0.20(1+0.20)^{5}}\right]=\$ 8,972
The present value of the difference in salvage values is determined by using Eq. (15-3) as follows:
P=\frac{F}{(1+i)^{n}} (15-3)
P_{ SV }=\frac{\$ 2,000}{(1+0.20)^{5}}=\$ 804
| Table 17-5 Cash Flow for Example 17-9 | ||||
| Cash Flow | Loader A ($) | Loader B ($) | Loader C ($) | Loader D ($) |
| Purchase Price | 110,000 | 127,000 | 120,000 | 130,000 |
| Annual Profit | 37,000 | 43,000 | 40,000 | 44,000 |
| Salvage Value | 10,000 | 13,000 | 12,000 | 13,000 |
The incremental net present value for the purchase of Loader C in lieu of Loader A is calculated as follows:
NPV =\$ 8,972+\$ 804+(-\$ 10,000)=-\$ 224
Because the incremental net present value is negative, Loader A continues to be the current best alternative. Next, we compare Loader A to Loader B, the loader with the next lowest initial cost.
The difference in the purchase price is $17,000 ($127,000 – $110,000). The difference in annual profit is $6,000 ($43,000 – $37,000). And the difference in salvage value is $3,000 ($13,000 – $10,000). The difference in the cash flows for these two alternatives is shown in Figure 17-8 .
The present value of the difference in annual profits is determined by using Eq. (15-9) as follows:
P_{ AP }=\$ 6,000\left[\frac{(1+0.20)^{5}-1}{0.20(1+0.20)^{5}}\right]=\$ 17,944
The present value of the difference in salvage values is determined by using Eq. (15-3) as follows:
P_{ SV }=\frac{\$ 3,000}{(1+0.20)^{5}}=\$ 1,206
The incremental net present value for the purchase of Loader B in lieu of Loader A is calculated as follows:
NPV =\$ 17,944+\$ 1,206+(-\$ 17,000)=\$ 2,150
Because the incremental net present value is positive, Loader B becomes the new current best alternative and Loader A is eliminated from comparison. Next, we compare Loader B to Loader D, the only remaining loader not compared.
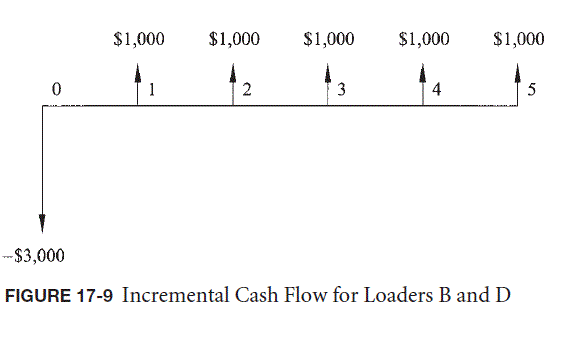
The difference in the purchase price is $3,000 ($130,000 – $127,000). The difference in annual profit is $1,000 ($44,000 – $43,000). And the difference in salvage value is zero ($13,000 – $13,000). The difference in the cash flows for these two alternatives is shown in Figure 17-9 .
The present value of the difference in annual profits is determined by using Eq. (15-9) as follows:
P_{ AP }=\$ 1,000\left[\frac{(1+0.20)^{5}-1}{0.20(1+0.20)^{5}}\right]=\$ 2,991
The incremental net present value for the purchase of Loader B in lieu of Loader D is calculated as follows:
NPV =\$ 2,991+\$ 0+(-\$ 3,000)=-\$ 9
Because the incremental net present value is negative, Loader B continues to be the current best alternative. With no other alternative to compare, Loader B is the selected alternative; therefore, your company should purchase Loader B.
When comparing two alternatives, the incremental net present value equals the difference between the NPVs for the alternatives. Let’s calculate the NPVs for Loader A and Loader C.
The present value of the annual profits for Loader A is determined by using Eq. (15-9) as follows:
P_{ AP }=\$ 37,000\left[\frac{(1+0.20)^{5}-1}{0.20(1+0.20)^{5}}\right]=\$ 110,653
The present value of the salvage value for Loader A is determined by using Eq. (15-3) as follows:
P_{ SV }=\frac{\$ 10,000}{(1+0.20)^{5}}=\$ 4,019
The NPV for the purchase of Loader A is calculated as follows:
NPV =\$ 110,653+\$ 4,019+(-\$ 110,000)=\$ 4,672
The present value of the annual profits for Loader C is determined by using Eq. (15-9) as follows:
P_{ AP }=\$ 40,000\left[\frac{(1+0.20)^{5}-1}{0.20(1+0.20)^{5}}\right]=\$ 119,624
The present value of the salvage values for Loader C is determined by using Eq. (15-3) as follows:
P_{ SV }=\frac{\$ 12,000}{(1+0.20)^{5}}=\$ 4,823
The NPV for the purchase of Loader C is calculated as follows:
NPV =\$ 119,624+\$ 4,823+(-\$ 120,000)=\$ 4,447