Question 10.3.2: Graphing a hyperbola opening up and down Determine the foci ...
Graphing a hyperbola opening up and down
Determine the foci and the equations of the asymptotes, and sketch the graph of
4 y^{2}-9 x^{2}=36.
Divide each side of the equation by 36 to get the equation into the standard form for the equation of the hyperbola:
\frac{y^{2}}{9}-\frac{x^{2}}{4}=1If x = 0, then y=\pm 3 . The y-intercepts are (0, 3) and (0, -3). Since b^{2}=4, the fundamental rectangle goes through the y-intercepts and through (2, 0) and (-2, 0). Draw the fundamental rectangle and extend its diagonals to get the asymptotes. Draw a hyperbola opening up and down from the y-intercepts approaching the asymptotes, as shown in Fig. 10.39. To find the foci, use c^{2}=a^{2}+b^{2} :
\begin{aligned} &c^{2}=9+4=13 \\ &c=\pm \sqrt{13} \end{aligned}The foci are (0, \sqrt{13}) and (0,-\sqrt{13}). From the fundamental rectangle, we can see that the equations of the asymptotes are
y=\frac{3}{2} x and y=-\frac{3}{2} x
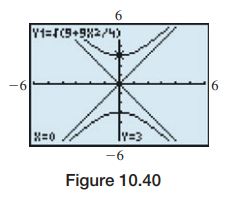
Check by graphing y=\pm \sqrt{9+9 x^{2} / 4} and y=\pm 1.5 x with a calculator, as shown in Fig. 10.40.
