Question 17.19: Your company is looking at purchasing a front-end loader at ...
Your company is looking at purchasing a front-end loader at a cost of $120,000. The loader can be billed out at $95.00 per hour. It costs $30.00 per hour to operate the front-end loader and $25.00 per hour for the operator. The useful life of the equipment is five years. The salvage value of the loader at the end of the fifth year is $12,000. Using 1,200 billable hours per year and a MARR of 20%. prepare a project balance graph for the front-end loader. What is the future worth of the loader? What is the payback period with interest?
Learn more on how we answer questions.
The hourly profit on the loader equals the billing rate less the operation cost and the cost of the operator, and is calculated as follows:
\text { Hourly Profit }=\$ 95.00 / hr -\$ 30.00 / hr -\$ 25.00 / hr
\text { Hourly Profit }=\$ 40.00 / hr
The annual profit on the loader equals the hourly profit times the number of billable hours per year and is calculated as follows:
\text { Annual Profit }=(\$ 40.00 / hr )(1,200 hr / yr )=\$ 48,000 / yr
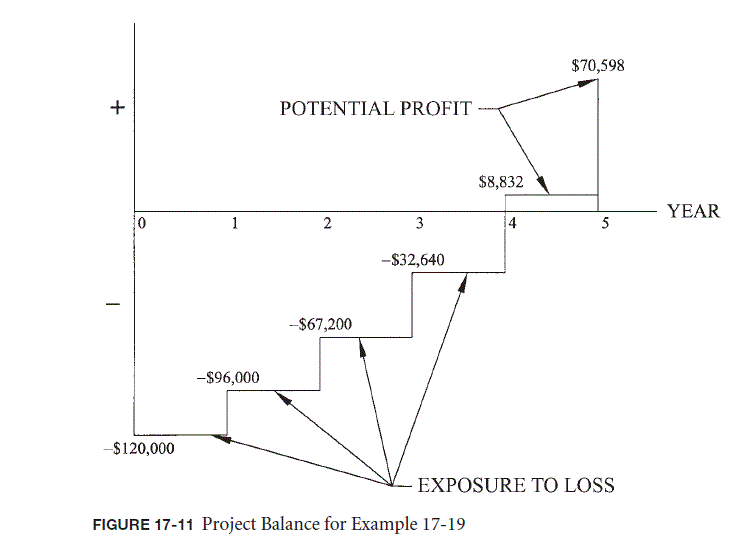
The project balance at the initial point in time ( t = 0) is a negative $120,000 or the cost of the front-end loader. If we were to terminate the investment immediately after the purchase of the loader, we would be exposed to a $120,000 loss less the equipment’s salvage value at the initial point in time.
The project balance at the end of the first year is equal to the project balance at the end of the previous period plus interest on the project balance from the previous period plus the annual profit. Because the project balance at the end of year 0 was negative the interest for period one will be negative. The project balance at the end of the first year is calculated as follows:
\begin{array}{l} PB _{1}= PB _{0}+ PB _{0}(i)+\text { Annual Profits } \\PB _{1}=-\$ 120,000+(-\$ 120,000)(0.20)+\$ 48,000 \\PB _{1}=-\$ 96,000\end{array}
The project balance at the end of the second year is equal to the project balance at the end of the previous period plus interest on the project balance from the previous period plus the annual profit. The project balance at the end of the second year is calculated as follows:
\begin{array}{l} PB _{2}=-\$ 96,000+(-\$ 96,000)(0.20)+\$ 48,000 \\PB _{2}=-\$ 67,200\end{array}
Similarly, the project balances at the end of the third and fourth years are calculated as follows:
\begin{array}{l} PB _{3}=-\$ 67,200+(-\$ 67,200)(0.20)+\$ 48,000=-\$ 32,640 \\PB _{4}=-\$ 32,640+(-\$ 32,640)(0.20)+\$ 48,000=\$ 8,832\end{array}
In the fifth year the annual profit is increased by the salvage value of the equipment or $12,000 for an annual profit of $60,000. The project balance at the end of the fifth year is calculated as follows:
PB _{5}=\$ 8,832+\$ 8,832(0.20)+\$ 60,000=\$ 70,598
The annual project balance for the loader may be graphed as shown in Figure 17-11 .
From the project balance graph, we see the payback period with interest is four years, which is the same as was calculated for this same loader in Example 17-18 . We also see that the loader has a future worth of $70,598, which is the same as was calculated in Example 17-10 . The onedollar difference is due to rounding.