Question 11.SP.18: The rotation of the 0.9-m arm OA about O is defined by the r...

STRATEGY: You are given information in terms of r and θ, so you should use polar coordinates.
MODELING and ANALYSIS: Model the collar as a particle.

Time t at which θ = 30°. Substitute θ = 30° = 0.524 rad into the expression for θ. You obtain

θ = 0.15t²             0.524 = 0.15t ²                           t = 1.869 s

Equations of Motion. Substituting t = 1.869 s in the expressions for r, θ, and their first and second derivatives, you have

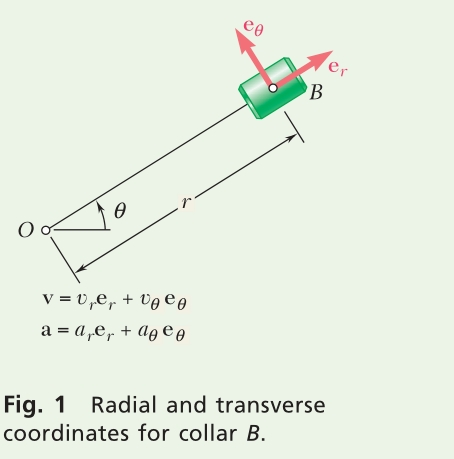
a. Velocity of B. Using Eqs. (11.44), you can obtain the values of v_{r} and  v_{θ}when t = 1.869 s (Fig. 1).

v_r=\dot{r}\qquad v_\theta=r \dot{\theta} (11.44)

Solve the right triangle shown in Fig. 2 to obtain the magnitude and direction of the velocity,

v = 0.524 m/s                                              β = 31.0°

b. Acceleration of B. Using Eqs. (11.45), you obtain (Fig. 3)

c. Acceleration of B with Respect to Arm OA. Note that the motion of the collar with respect to the arm is rectilinear and defined by the coordinate r (Fig. 4). You have

REFLECT and THINK: You should consider polar coordinates for any kind of rotational motion. They turn this problem into a straightforward solution, whereas any other coordinate system would make this problem much more difficult. One way to make this problem harder would be to ask you to find the radius of curvature in addition to the velocity and acceleration. To do this, you would have to find the normal component of the acceleration; that is, the component of acceleration that is perpendicular to the tangential direction defined by the velocity vector.