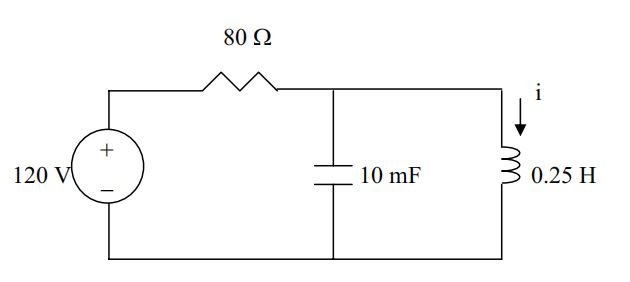
After being open for a day, the switch in the circuit of Fig. 8.99 is closed at t= 0 . Find the differential equation describing i(t), t > 0
Question 8.53: After being open for a day, the switch in the circuit of Fig...

The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
At t<0, i(0- )= 0, v_{c}(0- )= 120 v
For t >0, we have the circuit as shown below.
\frac{120-V}{R}=C \frac{d v}{d t}+i \quad \longrightarrow \quad 120=V+R C \frac{d v}{d t}+i R (1)
But v_{L}=v=L \frac{d i}{d t} (2)
Substituting ( 2 ) into (1) yields
120=L \frac{d i}{d t}+R C L \frac{d^{2} i}{d t^{2}}+i R \quad \longrightarrow \quad 120=\frac{1}{4} \frac{d i}{d t}+80 \times \frac{1}{4} \times 10 \times 10^{-3} \frac{d^{2} i}{d t^{2}}+80 i
or
\left(\mathrm{d}^{2} \mathrm{i} / \mathrm{d} \mathrm{t}^{2}\right)+0.125(\mathrm{di} / \mathrm{dt})+400 \mathrm{i}=600
Related Answered Questions
For t = 0-, v(0) = 0.
For t > 0, the circuit is...
The schematic is as shown below. The unit step is ...
The schematic is shown below. We use VPWL and IPWL...
The dual is constructed in Figure (a) and redrawn ...
The dual is obtained from the original circuit as ...
The dual circuit is connected as shown in Figure (...
\alpha=300=\frac{1}{2 R C} (1)[/latex...
Let i= inductor current and v= capacitor voltage.
...
For t = 0-, 4u(t) = 0, v(0) = 0, and i(0) = 30/10 ...
For \mathrm{t}=0^{-}, \mathrm{i}(0)=3+12 / ...