Question 6.3: Use of the frequency response function Find the waveform of ...

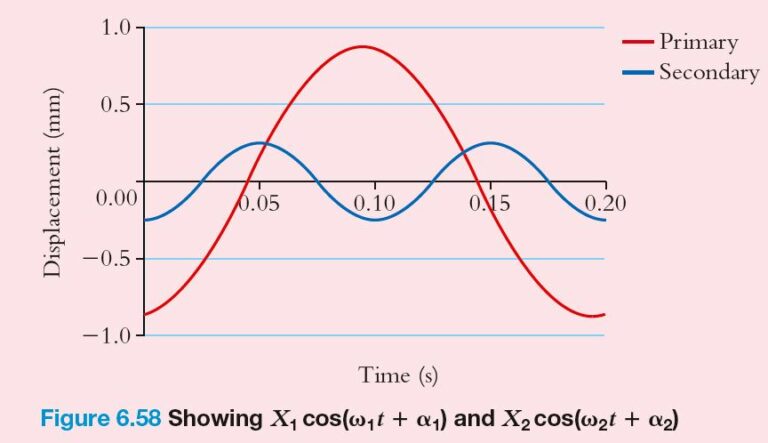
The compressor can be modelled as a rigid mass and its mounts as a spring–damper combination as shown in Figure 6.57. Each sinusoidal term in the excitation will produce a steady-state response that is sinusoidal with the same frequency as the excitation. For example, the term S_{1} \cos \omega _{1} t will produce a response in the form X_{1} \cos (\omega _{1} t + \alpha _{1}). We can use the frequency response function to do this.

Once the response to each excitation term has been found, the total response is obtained simply by adding the two together.

For each excitation term, we have X_{j}^{\star} = H(\omega _{j}) \times S_{j} so that X_{j} = \left|X_{j}^{\star}\right| = \left|H(\omega j)\right| \times S_{j} where j = 1 or 2. We can use the equations (6.50) and (6.51) to work out the FRF magnitude and phase angle values.

The FRF magnitude is             \left|H(\omega )\right| = \frac{1}{K} \frac{1}{\sqrt{\left(1  –  \frac{\omega ^{2}}{\omega ^{2}_{n}} \right)^{2} + 4\gamma ^{2} \frac{\omega ^{2}}{\omega ^{2}_{n}} } }                   (6.50)

and the phase angle is                 \alpha = \tan ^{- 1} \left(\frac{-  2 \gamma \frac{\omega }{\omega _{n}} }{1  –  \frac{\omega ^{2}}{\omega ^{2} _{n}} } \right)                                        (6.51)

Using the data given,

The term ‘primary’ relates to the fact that the vibration frequency, \omega _{1}, is equal to the rotational frequency of the crank. The ‘secondary’ component has a frequency that is twice the rotational frequency of the crank.