Question 13.2: Determine the view factors F12 and F21 for the following geo...
Determine the view factors F_{12} and F_{21} for the following geometries:
1. Sphere of diameter D inside a cubical box of length L = D.
2. One side of a diagonal partition within a long square duct.
3. End and side of a circular tube of equal length and diameter.

Learn more on how we answer questions.
Known: Surface geometries.
Find: View factors.
Assumptions: Diffuse surfaces with uniform radiosities.
Analysis: The desired view factors may be obtained from inspection, the reciprocity rule, the summation rule, and/or use of the charts.
1. Sphere within a cube:
By inspection, F_{12} = 1
By reciprocity, F_{21} = \frac{A_{1}}{A_{2}}F_{12} = \frac{\pi D^{2}}{6L^{2}} × 1 = \frac{\pi}{6}
2. Partition within a square duct:
From summation rule, F_{11} + F_{12} + F_{13} = 1
where F_{11} = 0
By symmetry, F_{12} = F_{13}
Hence F_{12} = 0.50
By reciprocity, F_{21} = \frac{A_{1}}{A_{2}}F_{12} = \frac{\sqrt{2}L}{L} × 0.5 = 0.71
3. Circular tube:
From Table 13.2 or Figure 13.5, with (r_{3}/L) = 0.5 and (L/r_{1}) = 2, F_{13} = 0.172
| TABLE 13.2 View Factors for Three-Dimensional Geometries [4] | |
| Geometry | Relation |
| Aligned Parallel Rectangles (Figure 13.4)
|
\overline{X} = X/L, \overline{Y} = Y/L\\ F_{ij} = \frac{2}{\pi \overline{X}\overline{Y}}\left\{\ln \left[\frac{(1 + \overline{X}^{2})(1 + \overline{Y}^{2})}{1 +\overline{X}^{2}+ \overline{Y}^{2}}\right]^{1/2} + \overline{X}(1 + \overline{Y}^{2})^{1/2} \tan^{-1}\frac{\overline{X}}{(1 + \overline{Y}^{2})^{1/2}} + \overline{Y}(1 + \overline{X}^{2})^{1/2} \tan^{-1}\frac{\overline{Y}}{(1 + \overline{X}^{2})^{1/2}} – \overline{X} \tan^{-1} \overline{X} – \overline{Y} \tan^{-1} \overline{Y}\right\} |
| Coaxial Parallel Disks (Figure 13.5)
|
R_{i} = r_{i}/L, R_{j} = r_{j}/L\\ S = 1 + \frac{1 + R^{2}_{j}}{R^{2}_{i}}\\ F_{ij} = \frac{1}{2} \left\{S – [S^{2} – 4(r_{j}/r_{i})^{2}]^{1/2}\right\} |
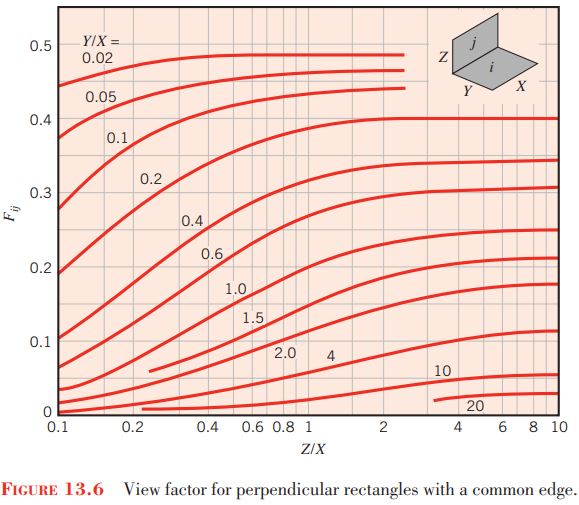
| Perpendicular Rectangles with a Common Edge (Figure 13.6)
|
H = Z/X, W = Y/X\\ F_{ij} = \frac{1}{\pi W} \left(W\tan^{-1} \frac{1}{W} + H \tan^{-1} \frac{1}{H} – (H^{2} + W^{2})^{1/2} \tan^{-1} \frac{1}{(H^{2} + W^{2})^{1/2}} + \frac{1}{4}\ln \left\{\frac{(1 + W^{2})(1 + H^{2})}{1 + W^{2} + H^{2}}\left[\frac{W^{2}(1 + W^{2} + H^{2})}{(1 + W^{2})(W^{2} + H^{2})}\right]^{W^{2}} \times \left[\frac{H^{2}(1 + H^{2} + W^{2})}{(1 + H^{2})(H^{2} + W^{2})}\right]^{H^{2}}\right\} \right) |
From summation rule, F_{11} + F_{12} + F_{13} = 1
or, with F_{11} = 0, F_{12} = 1 – F_{13} = 0.828
From reciprocity, F_{21} = \frac{A_{1}}{A_{2}}F_{12} = \frac{\pi D^{2}/4}{\pi DL} × 0.828 = 0.207
Comment: The geometric surfaces may, in reality, not be characterized by uniform radiosities. The consequences of nonuniform radiosity are discussed in Example 13.3.