Question 5.4: Determine the location of the centroid of a parabolic spandr...
Determine the location of the centroid of a parabolic spandrel by direct integration.

Learn more on how we answer questions.
STRATEGY: First express the parabolic curve using the parameters a and b. Then choose a differential element of area and express its area in terms of a, b, x, and y. We illustrate the solution first with a vertical element and then a horizontal element.
MODELING:
Determination of the Constant k. Determine the value of k by substituting x = a and y = b into the given equation. We have b = ka² or k = b/a². The equation of the curve is thus
y=\frac{b}{a^2}x^2 \quad \quad \quad \text{ or } \quad \quad \quad x=\frac{a}{b^{1/2}}y^{1/2}
ANALYSIS:
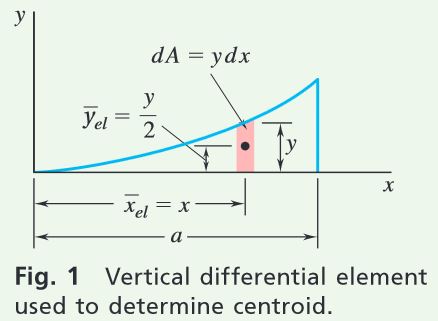
Vertical Differential Element. Choosing the differential element shown in Fig. 1, the total area of the region is
A=\int{dA}=\int{y \ dx}=\int_{0}^{a}{\frac{b}{a^2}x^2 }\;dx =\left[\frac{b}{a^2}\frac{x^3}{3} \right]^a_0 =\frac{ab}{3}
The first moment of the differential element with respect to the y axis is \bar{x}_{el} dA; hence, the first moment of the entire area with respect to this axis is
Q_y=\int{\bar{x}_{el}} \ dA=\int{xy \ dx=\int_{0}^{a}{x\left(\frac{b}{a^2}x^2 \right) }\;dx } =\left[\frac{b}{a^2}\frac{x^4}{4} \right]^a_0=\frac{a^2b}{4}
Since Q_y=\bar{x}A, you have
\bar{x}A=\int{\bar{x}_{el} \ dA} \quad \quad \quad \bar{x}\frac{ab}{3}=\frac{a^2b}{4} \quad \quad \quad \bar{x}=\frac{3}{4}a
Likewise, the first moment of the differential element with respect to the x axis is \bar{y}_{el}dA, so the first moment of the entire area about the x axis is
Q_x=\int{\bar{y}_{el} \ dA}=\int{\frac{y}{2}y \ dx }=\int_{0}^{a}{\frac{1}{2} \left(\frac{b}{a^2}x^2 \right)^2 }\;dx =\left[\frac{b^2}{2a^4}\frac{x^5}{5} \right]^a_0=\frac{ab^2}{10}
Since Q_x=\bar{y}A, you get
\bar{y}A=\int{\bar{y}_{el}}dA \quad \quad \quad \quad \quad \bar{y}\frac{ab}{3} =\frac{ab^2}{10} \quad \quad \quad \quad \quad \bar{y}=\frac{3}{10}b
Horizontal Differential Element. You obtain the same results by considering a horizontal element (Fig. 2). The first moments of the area are
\begin{matrix} Q_y=\int{\bar{x}_{el}}dA=\int{\frac{a+x}{2}(a-x)dy }=\int_{0}^{b}{ \frac{a^2-x^2}{2}dy} \\ =\frac{1}{2}\int_{0}^{b}{\left(a^2-\frac{a^2}{b}y\right) }\;dy=\frac{a^2b}{4} \\ Q_x=\int{\bar{y}_{el}dA}=\int{y(a-x)}dy=\int{y\left(a-\frac{a}{b^{1/2}}y^{1/2} \right)dy } \\=\int_{0}^{b}{\left(ay-\frac{a}{b^{1/2}}y^{3/2} \right)dy }=\frac{ab^2}{10} \end{matrix}
To determine \bar{x} \text{ and } \bar{y}, again substitute these expressions into the equations defining the centroid of the area.
REFLECT and THINK: You obtain the same results whether you choose a vertical or a horizontal element of area, as you should. You can use both methods as a check against making a mistake in your calculations.