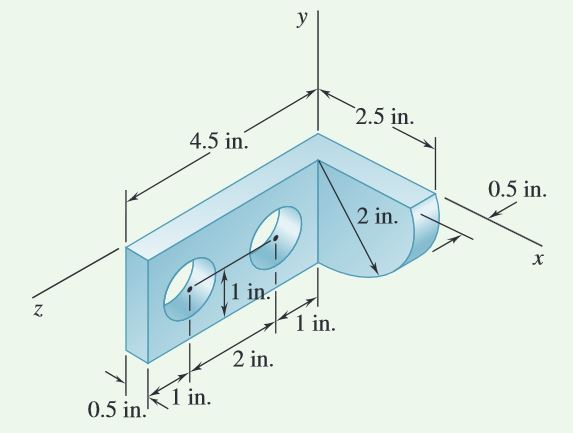
Question 5.11: Locate the center of gravity of the steel machine part shown...
Locate the center of gravity of the steel machine part shown. The diameter of each hole is 1 in.
Learn more on how we answer questions.
STRATEGY: This part can be broken down into the sum of two volumes minus two smaller volumes (holes). Find the volume and centroid of each volume and combine them using Eq. (5.20) to find the overall centroid.
\bar{X}\sum{V}=\sum{\bar{x}}V \quad \quad \quad \bar{Y}\sum{V}=\sum{\bar{y}}V \quad \quad \quad \bar{Z}\sum{V}=\sum{\bar{z}}V \quad \quad \quad \quad \quad (5.20)
MODELING: As shown in Fig. 1, the machine part can be obtained by adding a rectangular parallelepiped (I) to a quarter cylinder (II) and then subtracting two 1-in.-diameter cylinders (III and IV). Determine the volume and the coordinates of the centroid of each component and enter them in a table (below). Using the data in the table, determine the total volume and
the moments of the volume with respect to each of the coordinate planes.
ANALYSIS: You can treat each component volume as a planar shape using Fig. 5.8A to find the volumes and centroids, but the right-angle joining of components I and II requires calculations in three dimensions. You may find it helpful to draw more detailed sketches of components with the centroids carefully labeled (Fig. 2).
| \pmb{\bar{z}}\pmb{V},\pmb{\text{in}^4} | \pmb{\bar{y}}\pmb{V},\pmb{\text{in}^4} | \pmb{\bar{x}}\pmb{V},\pmb{\text{in}^4} | \pmb{\bar{z}},\pmb{\text{in.}} | \pmb{\bar{y}},\pmb{\text{in.}} | \pmb{\bar{x}},\pmb{\text{in.}} | \pmb{V},\pmb{\text{in.}}^3 | |
| 10.125 | -4.5 | 1.125 | 2.25 | -1 | 0.25 | (4.5)(2)(0.5) =4.5 | I |
| 0.393 | -1.333 | 2.119 | 0.25 | -0.8488 | 1.3488 | \frac{1}{4}\pi(2)^2(0.5)=1.571 | II |
| -1.374 | 0.393 | -0.098 | 3.5 | -1 | 0.25 | -\pi(0.5)^2(0.5)=-0.3927 | III |
| -0.589 | 0.393 | -0.098 | 1.5 | -1 | 0.25 | -\pi(0.5)^2(0.5)=-0.3927 | IV |
| \sum{\bar{z}V}=8.555 | \sum{\bar{y}V}=-5.047 | \sum{\bar{x}V}=3.048 | ΣV=5.286 |
Thus,
\bar{X}\sum{V}=\sum{\bar{x}V}: \quad \quad \quad \bar{X}(5.286 \text{ in}^3)=3.048 \text{ in}^4 \quad \quad \quad \quad \bar{X}=0.577 \text{ in}. \\ \bar{Y}\sum{V}=\sum{\bar{y}V}: \quad \quad \quad \bar{Y}(5.286 \text{ in}^3)=-5.047 \text{ in}^4 \quad \quad \quad \quad \bar{Y}=-0.955 \text{ in}. \\ \bar{Z}\sum{V}=\sum{\bar{z}V}: \quad \quad \quad \bar{Z}(5.286 \text{ in}^3)=8.555 \text{ in}^4 \quad \quad \quad \quad \bar{Z}=1.618 \text{ in}.REFLECT and THINK: By inspection, you should expect \bar{X} \text{ and } \bar{Z} to be considerably less than (1/2)(2.5 in.) and (1/2)(4.5 in.), respectively, and Y to be slightly less in magnitude than (1/2)(2 in.). Thus, as a rough visual check, the results obtained are as expected.


