Question 10.1: Shaft BC is hollow with inner and outer diameters of 90 mm a...

STRATEGY: Use free-body diagrams to determine the torque in each shaft. The torques can then be used to find the stresses for shaft BC and the required diameters for shafts AB and CD.
MODELING: Denoting by \pmb{\text{T}}_{AB} the torque in shaft AB (Fig. 1), we pass a section through shaft AB and, for the free body shown, we write

\sum M_x=0: \quad \quad \quad (6 \text{ kN.m})-T_{AB}=0 \quad \quad T_{AB}=6 \text{ kN.m}

We now pass a section through shaft BC (Fig. 2) and, for the free body shown, we have

\sum M_x=0: \quad \quad (6 \text{ kN.m})+(14 \text{ kN.m})-T_{BC}=0 \quad \quad T_{BC}=20 \text{ kN.m}

ANALYSIS:
a. Shaft BC. For this hollow shaft we have

J=\frac{\pi}{2}(c^4_2 – c^4_1) = \frac{\pi}{2}[(0.060)^4-(0.045)^4]=13.92 \times 10^{-6} \text{ m}^4

Maximum Shearing Stress.       On the outer surface, we have

\tau_{max}=\tau_2=\frac{T_{BC}c_2}{J}=\frac{(20 \text{ kN.m})(0.060 \text{ m})}{13.92 \times 10^{-6} \text{ m}^4} \quad \quad \quad \tau_{max}=86.2 \text{ MPa}

Minimum Shearing Stress.        As shown in Fig. 3 the stresses are proportional to the distance from the axis of the shaft.

\frac{\tau_{min}}{\tau_{max}} =\frac{c_1}{c_2} \quad \quad \quad \frac{\tau_{min}}{86.2 \text{ MPa}} =\frac{45 \text{ mm}}{60 \text{ mm}} \quad \quad \quad \tau_{min} =64.7 \text{ MPa}

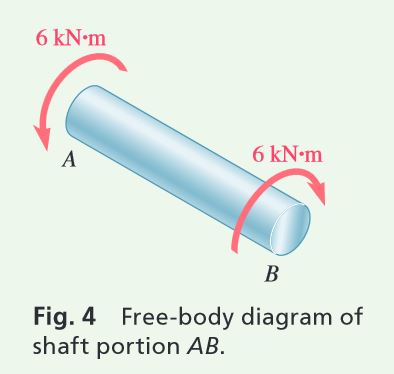
b. Shafts AB and CD. We note that both shafts have the same torque T = 6 kN.m (Fig. 4). Denoting the radius of the shafts by c and knowing that \tau_{\text{all}} = 65 \text{ MPa }, we write

\tau=\frac{T_c}{J} \quad \quad \quad 65 \text{ MPa}=\frac{(6 \text{ kN.m})c}{\frac{\pi}{2}c^4 } \\ c^3=58.8 \times 10^{-6} \text{m}^3 \quad \quad c=38.9 \times 10^{-3} \text{ m} \\ d=2c=2(38.9 \text{ mm}) \quad \quad \quad \quad d=77.8 \text{ mm}