Question 8.10: Find the root sensitivity of the system in Figure 8.4 at s =...
Find the root sensitivity of the system in Figure 8.4 at s = − 9.47 and −5 + j5. Also calculate the change in the pole location for a 10% change in K.
Learn more on how we answer questions.
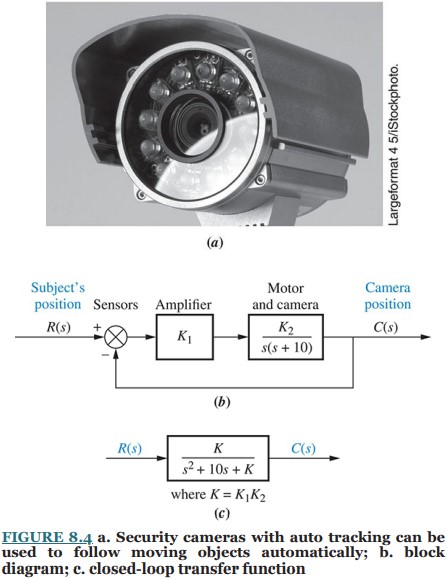
The system’s characteristic equation, found from the closed-loop transfer function denominator, is s² + 10s + K = 0. Differentiating with respect to K, we have
2s \frac{\delta s}{\delta K} + 10 \frac{\delta s}{\delta K} + 1 = 0 (8.71)
from which
\frac{\delta s}{\delta K} = \frac{-1}{2s + 10} (8.72)
Substituting Eq. (8.72) into Eq. (8.69), the sensitivity is found to be
S_{s :K} = \frac{K}{s} \frac{\delta s}{\delta K} (8.69)
S_{s :K} = \frac{K}{s} × \frac{-1}{2s + 10} (8.73)
For s = − 9.47, Table 8.1 shows K = 5. Substituting these values into Eq. (8.73) yields S_{s :K} = − 0.059. The change in the pole location for a 10% change in K can be found using Eq. (8.70), with s = − 9.47, Δ K/K = 0.1, and S_{s :K} = − 0.059. Hence, Δ_{s} = 0.056, or the pole will move to the right by 0.056 units for a 10% change in K.
TABLE 8.1 Pole location as function of gain for the system of Figure 8.4
| K | Pole 1 | Pole 2 |
| 0 | −10 | 0 |
| 5 | −9.47 | −0.53 |
| 10 | −8.87 | −1.13 |
| 15 | −8.16 | −1.84 |
| 20 | −7.24 | −2.76 |
| 25 | −5 | −5 |
| 30 | − 5 + j2.24 | − 5 – j2.24 |
| 35 | − 5 + j3.16 | − 5 – j3.16 |
| 40 | − 5 + j3.87 | − 5 – j3.87 |
| 45 | − 5 + j4.47 | − 5 – j4.47 |
| 50 | − 5 + j5 | − 5 – j5 |
Δ_{s} = s(S_{s :K}) \frac{ΔK}{K} (8.70)
For s = − 5 + j5, Table 8.1 shows K = 50. Substituting these values into Eq. (8.73) yields S_{s :K} = 1/ (1 + j1) = (1/\sqrt{2} ) ∠ − 45°. The change in the pole location for a 10% change in K can be found using Eq. (8.70), with s = − 5 + j5, Δ K/K = 0.1, and S_{s :K} = (1/\sqrt{2} ) ∠ − 45°. Hence, Δ_{s} = − j5, or the pole will move vertically by 0.5 unit for a 10% change in K.
In summary, then, at K = 5, S_{s :K} = − 0.059. At K = 50, S_{s :K} = (1/\sqrt{2} ) ∠ − 45°. Comparing magnitudes, we conclude that the root locus is less sensitive to changes in gain at the lower value of K. Notice that root sensitivity is a complex quantity possessing both the magnitude and direction information from which the change in poles can be calculated.