Question 5.13: Inductor Current and Voltage Consider the circuit shown in F...

Electrical Engineering: Concepts and Applications

Inductor Current and Voltage

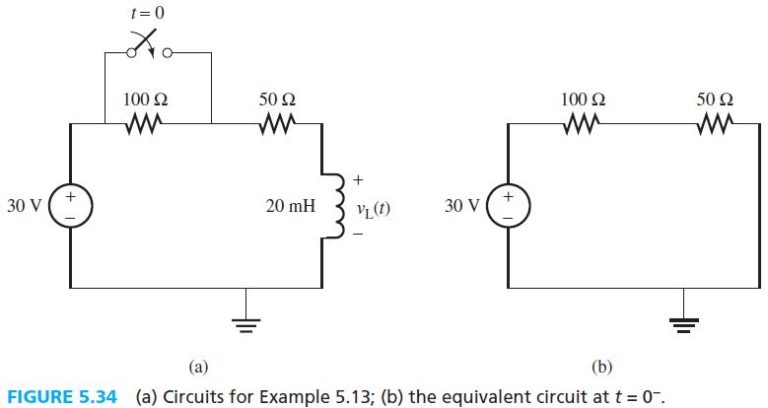
Consider the circuit shown in Figure 5.34. The switch closes at t = 0 after being opened for a long time period. Find $i_{L}\left(0^{+}\right), v_{L}\left(0^{+}\right)$ , and $i_{L}(\infty)$ .

5.13

The blue check mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.

For t < 0, the switch is open for a long time period. Therefore, the inductor can be represented by a short circuit and the equivalent circuit is shown in Figure 5.34(b). The inductor current can be calculated as follows:

\begin{aligned}i_{L}\left(0^{+}\right)=i_{L}\left(0^{-}\right) &=\frac{30}{100+50} \\&=0.2  A\end{aligned}

Closing the switch short-circuits the 100-Ω resistor. As a result:

\begin{aligned}v_{L}\left(0^{+}\right) &=30-50 \times i_{L}\left(0^{+}\right) \\&=30-50 \times 0.2 \\&=20  V\end{aligned}

At t = ∞ , or steady state, the inductor becomes a short circuit. Thus:

i_{L}(\infty)=\frac{30}{50}=0.6  A

Related Answered Questions

Question: 5.9

Inductor Current Find an expression for iL (t) in the circuit shown in Figure 5.28. Assume the switch has been closed for a long time and opens at t = 0. ...

Verified Answer:

KCL for Node A corresponds to:

-i_{s}+i_{R}...

Question: 5.10

Inductor Voltage Find an expression for vL (t) in the circuit shown in Figure 5.29. Switch is opened at t = 0 after being closed for a long time. ...

Verified Answer:

This problem can be solved in a way similar to the...

Question: 5.11

DC Motor A motor, when switched on, does not immediately attain its final speed. This is due to the inductance of the motor coils. A DC motor is connected as shown in Figure 5.30 (a) and its model is shown in Figure 5.30 (b). Assume an inductor with zero initial charge (or assume the switch is open ...

Verified Answer:

a. The inductor is an open circuit at t = 0; thus,...

Question: 5.12

Explosive Atmosphere When working in a hazardous, explosive atmosphere, workers must ensure that equipment does not produce any sparks that may lead to an explosion. At a minimum, any sparks must be isolated from the surrounding environment. Chapter 15 outlines how even a simple flashlight can ...

Verified Answer:

Before opening the switch (i.e., t < 0), the ci...

Question: 5.14

Initial and Final Voltage and Current Consider the circuit shown in Figure 5.36. Find vC(0^+), iC(0^+), and vC(∞). ...

Verified Answer:

The equivalent circuit at

t=0^{+}

(a...

Question: 5.15

Series RLC Circuit The DC voltage source of the circuit shown in Figure 5.38 is connected to the series RLC circuit by closing the switch at t = 0. The initial conditions are: iL(0) = 0 and vC(0) = 0. Find the voltage and the current across the capacitor if: a. R = 60 Ω b. R = 40 Ω c. R = 30 Ω ...

Verified Answer:

To find the circuit's conditions, calculate parame...

Question: 5.8

Gyro Sensor The purpose of the gyro is to detect and determine the orientation of an object to which it is attached. These systems have applications in self-localization such as Inertial Navigation Systems (INS), used in aeronautical systems, boats, etc. This allows a vehicle (mobile) to find its ...

Verified Answer:

Using the definition of

v_{C}(t)=V_{S}\left...

Question: 5.5

Light Timer RC circuits can be used to build simple timers. Figure 5.17 shows a circuit that turns off a light after a given period of time. The transistor Q1 and the relay ensure that the light goes from fully ON to fully OFF. Transistor circuits are discussed in detail in Chapter 8. When the ...

Verified Answer:

In Figure 5.18, the switch has been closed for a l...

Question: 5.4

Capacitor Voltage The switch in the circuit shown in Figure 5.16 has stayed in position 1 for a long time period. At time t = 0 the switch moves to position 2. a. Find v1 (0^-), that is, v1 (t) prior to the displacement of the switch. b. Find v2 (0^+), that is, v2 (t) right after the displacement ...

Verified Answer:

a. After a long time period of the switch being in...

Question: 5.3

Capacitor Voltage The switch in the circuit shown in Figure 5.11 has been closed for a long time period and opens at t = 0. a. Find an expression for vC(t) b. Find the capacitor voltage after 60 ms c. Find vC(t) when t tends to infinity ...

Verified Answer:

Because the switch was closed for a long time, the...