Question 20.13: A rigid body of mass M is free to rotate about a horizontal ...

i) The weight is the force which makes the body rotate about the axis. When it is in the position shown in figure 20.32, the moment of the weight about the axis in the direction of increasing θ is – Mgl sin θ.

The work done by gravity when θ decreases from α to zero is therefore

\int_{α}^{0}{- Mgl  sin  θ dθ} = \left[Mgl  cos  θ \right]^{0}_{α}

= Mgl(1 – cos α).

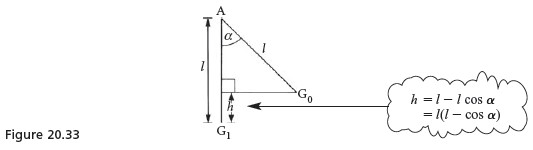
But the height fallen by G is h = l(1 – cos α ), see figure 20.33. Hence the work done by gravity is equal to Mgh, the loss in potential energy of a particle of mass M which has fallen the same height as G.

ii) By the work–energy equation, or the principle of conservation of energy, the kinetic energy gained when AG is vertical is given by

\frac{1}{2}I\dot{θ}^{2} = Mgh

The angular speed at this point is then

\sqrt{\frac{2Mgh}{I}} = \sqrt{\frac{2Mgl}{I} (1  –  cos  α).}

Note
The assumption that the potential energy of a large body is the same as that of a particle of equal mass situated at G follows from the definition of G. If Oy is the co-ordinate axis in the vertical direction, then

M\bar{y} = \sum{(m_{p}y_{p})}      ⇒      Mg\bar{y} = ∑(m_{p}gy_{p}).