Question 4.2: Determine the dimensioning schematic to obtain a better accu...
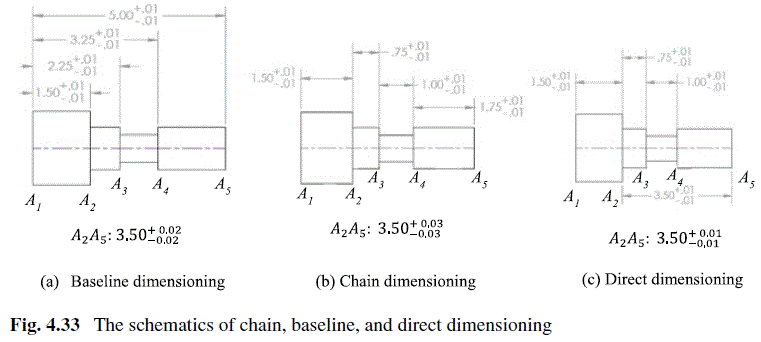
Determine the dimensioning schematic to obtain a better accuracy of the dimension A_{2} A_{5} in Fig. 4.33.
For the baseline dimensioning in Fig. 4.33a, the dimension of A_{2} A_{5} is indirectly derived as\left.\begin{matrix}Norminal of A_{2}A_{5} = A_{1}A_{5} – A_{1}A_{2} = 3.50 \\\ Tolerance of A_{2}A_{5} = \begin{matrix} Upper limi t of A_{1}A_{5} – Lower limi t of A_{1}A_{2} \\ Lower limi t of A_{1}A_{5} – Upper limi t of A_{1}A_{2} \end{matrix}=\begin{matrix} +0.02 \\ -0.02 \end{matrix} \end{matrix} \right\} (4.8)
For the chain dimensioning in Fig. 4.33b, the dimension of A_{2} A_{5} is indirectly derived as
\left.\begin{matrix}Norminal of A_{2}A_{5} = A_{2}A_{3} + A_{3}A_{4} + A_{4}A_{5} = 3.50 \\\ Tolerance of A_{2}A_{5} = \begin{matrix} Upper limi t of A_{2}A_{3} + A_{3}A_{4} + A_{4}A_{5} \\ Lower limi t of A_{2}A_{3} + A_{3}A_{4} + A_{4}A_{5} \end{matrix} = \begin{matrix} +0.03 \\ -0.03 \end{matrix} \end{matrix} \right\} (4.9)For the direct dimensioning in Fig. 4.33c, the dimension of A_{2} A_{5} is directly obtained as A_{2} A_{5} : 3.50^{+0.01}_{-0.01} . By comparing the tolerances of A_{2} A_{5} in three schematics, direct dimensioning yields the most accuracy for the dimension A_{2} A_{5}.