Question 5.p.4: Using the probabilities of .60 for a new bridge and .40 for ...
Using the probabilities of .60 for a new bridge and .40 for no new bridge:
a. Compute the expected value of each alternative in the payoff table, and identify the alternative that would be selected under the expected-value approach.
b. Construct a decision tree for the problem showing expected values.
The blue check mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
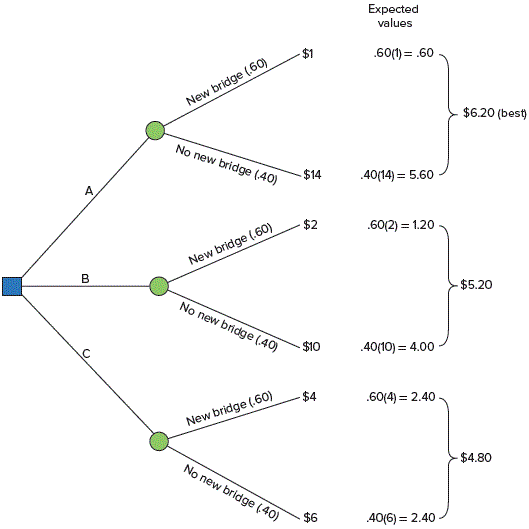
a. A: .60(1) + .40(14) = 6.20 [best]
B: .60(2) + .40(10) = 5.20
C: .60(4) + .40(6) = 4.80
b.
Related Answered Questions
Question: 5.p.5
Verified Answer:
The attainable output of each portion of the syste...
Question: 5.p.6
Verified Answer:
a.
New
Bridge
No New
Bridge
Maximin
(worst)
M...
Question: 5.p.5
Verified Answer:
Using Formula 5S-1, the EVPI is the expected payof...
Question: 5.p.3
Verified Answer:
To obtain the regrets, subtract all payoffs in eac...
Question: 5.p.2
Verified Answer:
Plot a straight line for each alternative. Do this...
Question: 5.p.1
Verified Answer:
New
Bridge
No New
Bridge
Maximin
(worst)
Maximax
(...
Question: 5.s-8
Verified Answer:
First, plot each alternative relative to P(2). To ...
Question: 5.s-7
Verified Answer:
Using information from Examples 5S–2, 5S–3, and 5S...
Question: 5.s-6
Verified Answer:
First, compute the expected payoff under certainty...
Question: 5.s-5
Verified Answer:
The dollar amounts at the branch ends indicate the...