Question 7.6.2: Solving a Trigonometric Equation (Zero-Factor Property) Solv...

\sin θ \tan θ = \sin θ               Original equation

\sin θ \tan θ – \sin θ = 0          Subtract \sin θ.

\sin θ(\tan θ – 1) = 0                Factor out \sin θ.

\sin θ = 0  \text{or}  \tan θ – 1 = 0      Zero-factor property

\tan  θ = 1

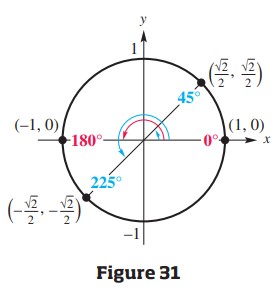
θ = 0°    or     θ = 180°    θ = 45°     or θ = 225°   Apply the inverse function.

See Figure 31. The solution set is {0°, 45°, 180°, 225°}.