Question 17.SP.8: A uniform sphere with a mass m and a radius r is projected a...
A uniform sphere with a mass m and a radius r is projected along a rough horizontal surface with a linear velocity \overline{\mathbf{v}}_1 and no angular velocity. Denote the coefficient of kinetic friction between the sphere and the surface by μ_k. Determine (a) the time t2 at which the sphere starts rolling without sliding, (b) the linear and angular velocities of the sphere at time t_2.
STRATEGY: You are asked to find the time, so use the principle of impulse and momentum. You can apply this principle to the sphere from the time t_1 = 0 when it is placed on the surface until the time t_2 = t when it starts rolling without sliding.
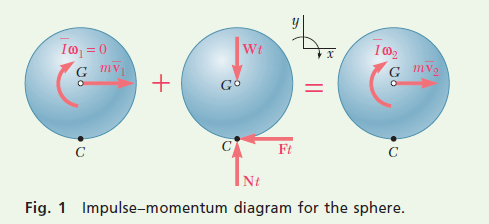
MODELING: Choose the sphere as your system and model it as a rigid body. While the sphere is sliding relative to the surface, it is acted upon by the normal force N, the friction force F, and its weight W with a magnitude of W = mg. An impulse-momentum diagram for this system is shown in Fig. 1.

Learn more on how we answer questions.
ANALYSIS:
Principle of Impulse and Momentum. Apply the principle of impulse and momentum for this system between time t_1 and t_2
\text { Syst Momenta }{ }_1 + \text { Syst Ext } \operatorname{Imp}_{1 \rightarrow 2}=\text { Syst Momenta }{ }_2
+\uparrow y \text { components: } \quad N t – W t=0 (1)
\stackrel{+}{\rightarrow} x \text { components: } \quad m \bar{v}_1 – F t=m \bar{v}_2 (2)
+\circlearrowright \text { moments about } G: \quad \quad \text { Ftr }=\bar{I} \omega_2 (3)
From Eq. (1) you obtain N = W = mg. During the entire time interval considered, sliding occurs at point C, and F=\mu_k N=\mu_k m g. Substituting this expression for F into Eq. (2), you have
m \bar{v}_1 – \mu_k m g t=m \bar{v}_2 \quad \bar{v}_2=\bar{v}_1 – \mu_k g t (4)
Substituting F=\mu_k m g and \bar{I}=\frac{2}{5} m r^2 into Eq. (3) gives
\mu_k m g t r=\frac{2}{5} m r^2 \omega_2 \omega_2=\frac{5}{2} \frac{\mu_k g}{r} t (5)
The sphere starts rolling without sliding when the velocity \mathbf{v}_C of the point of contact is zero. At that time, point C becomes the instantaneous center of rotation, and you have \bar{v}_2=r \omega_2. Substituting Eqs. (4) and (5) into this equation, you obtain
\bar{v}_1 – \mu_k g t=r\left(\frac{5}{2} \frac{\mu_k g}{r} t\right) \quad t=\frac{2}{7} \frac{\bar{v}_1}{\mu_k g}
Substituting this expression for t into Eq. (5), you have
\omega_2=\frac{5}{2} \frac{\mu_k g}{r}\left(\frac{2}{7} \frac{\bar{v}_1}{\mu_k g}\right) \quad \omega_2=\frac{5}{7} \frac{\bar{v}_1}{r} \quad \omega_2=\frac{5}{7} \frac{\bar{v}_1}{r} \circlearrowright
\bar{v}_2=r \omega_2 \quad \bar{v}_2=r\left(\frac{5}{7} \frac{v_1}{r}\right) \quad \overline{\mathbf{v}}_2=\frac{5}{7} \bar{v}_1 \rightarrow
REFLECT and THINK: This is the same answer obtained in Sample Prob. 16.6 by first dealing directly with force and acceleration and then applying kinematic relationships.