Question 7.21: Prove that the ratio of depth to width of the strongest beam...

Given :
Dia. of log = d
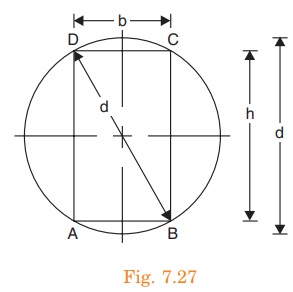
Let ABCD be the strongest rectangular section which can be cut out of the cylindrical log.
Let b = Width of strongest section.
d = Depth of strongest section.

Now section modulus of the rectangular section

Z=\frac{I}{y}=\frac{(\frac{bh^3}{12})}{(\frac{h}{2})}=\frac{bh^2}{6}      …(i)

In the above equation, b and h are variable.
From ∆BCD, b² + h² = d²
or                     h² = d² – b²

Substituting the value of h² in equation (i), we get

Z=\frac{b}{6}[d^2-b^2]=\frac{1}{6}[bd^2-b^3]                 …(ii)

In the above equation, d is constant and hence only variable is b.
Now for the beam to be strongest, the section modulus should be maximum (or Z should be maximum).
For maximum value of Z,

\frac{dZ}{db}=0

or     \frac{d}{db}=[\frac{bd^2-b^3}{6}]=0 \quad \text{ or } \quad \frac{d^2-3b^2}{6}=0

or      d² – 3b² = 0     or     d² = 3b²      …(iii)

But from triangle BCD,

d² = b² + h²

Substituting the value of d² in equation (iii), we get

b² + h² = 3b²     or    h² = 2b²

or       h=\sqrt{2}\times b              …(iv)

or       \frac{h}{b}=\sqrt{2}=\pmb{1.414.}

Numerical Part

Given, d = 300 mm
But for equation (iii), d² = 3b²    or    3b² = d² = 300² = 90000

or              b^2=\frac{90000}{3}=30000

∴                b=(30000)^{1/2}=\pmb{173.2  mm.}

From equation (iv),

h=\sqrt{2}\times b=1.414 × 173.2 = \pmb{249.95  mm.}