Question 6.3: A compound beam made of two bars AC and CD hinged together a...

From the free-body diagram shown in Figure 6.13(a).

R_{ A }+R_{ B }+R_{ D }=9 w            (1)

From free-body diagram shown in Figure 6.13(c), we get for equilibrium:

\sum M_{ C }=0, \quad 3 R_{ D }=3 w \times \frac{3}{2}

or              R_{ D }=\frac{3 w}{2}              (2)

Similarly, from free-body diagram shown in Figure 6.13(b), \Sigma M_{ C }=0 ,

or          -R_{ A } \times 6-R_{ B } \times 3+6 w \times \frac{6}{2}=0

2 R_{ A }+R_{ B }=6 w              (3)

From Eqs. (1)–(3), we find, R_{ A }, R_{ B } \text { and } R_{ D } . Hence, we get

R_{ A }=\frac{3 w}{2}(\downarrow), \quad R_{ B }=9 w(\uparrow) \quad \text { and } \quad R_{ D }=\frac{3 w}{2}(\uparrow)

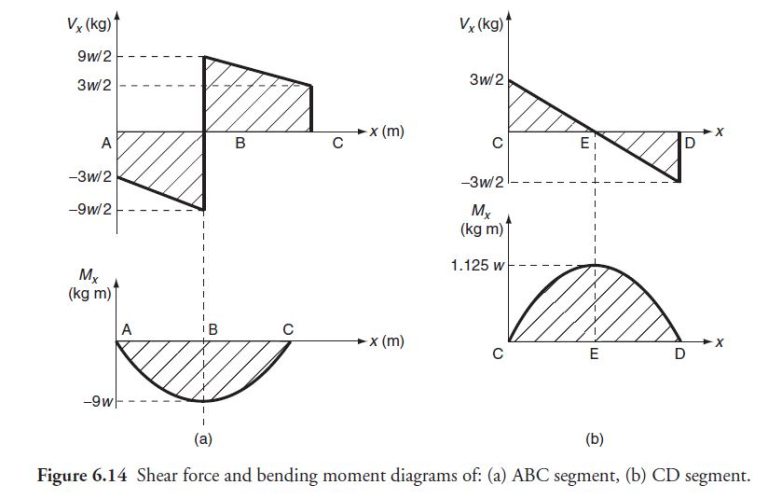
Putting values of R_{ A }, R_{ B } \text { and } R_{ D } and drawing shear force and bending moment diagrams as shown in Figure 6.14, we get the following results:

\begin{aligned} & M_{ B }=9 w  kg  m \\ & M_{ C }=0 \\ & M_{ E }=1.125 w  kg  m \end{aligned}

\text { So, } M_{\max }=9 w  kg  m . The maximum bending stress is

\sigma_{\max }=\frac{9 w}{Z}=\frac{9 w \times 100}{71.8}  kg  cm / cm ^3             (given that  Z = 71.8 cm³).

Equating with working stress, 1400 kg/cm², we get

\frac{9 w \times 100}{71.8}=1400

or w = 111.69 kg/m. So, the safe value of load-intensity is 111.69 kg/m.