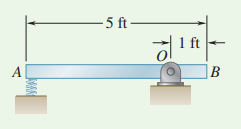
Question 17.SP.4: A 30-lb slender rod AB is 5 ft long and is pivoted about a p......

STRATEGY: Because you are given two positions, want to find the velocities, and no external forces do work, use the conservation of energy. To determine the reactions at position 2, use a free-body diagram and a kinetic diagram.

MODELING: Choose the rod and the spring as your system and model the rod as a rigid body. Denote the initial position as position 1 and the vertical position as position 2 (Fig. 1). Choose your datum to be at position 1.

ANALYSIS:

Conservation of Energy.

T_1+V_{g_1}+V_{e_1}=T_2+V_{g_2}+V_{e_2}           (1)

You need to calculate the energy at position 1 and position 2.

Position 1.

Potential Energy. The spring is compressed 1 in., so you have x_1 = 1 in. The elastic potential energy is

V_{e_1}=\frac{1}{2} k x_1^2=\frac{1}{2}(1800~lb / in .)(1~in .)^2=900~in . \cdot lb =75 ft \cdot lb

Because the datum is at position 1, you have V_{g_1} = 0.

Kinetic Energy. The velocity in position 1 is zero, so you have T_1 = 0.

Position 2.

Potential Energy. The elongation of the spring is zero, so you have V_{e_2} = 0.
Because the center of gravity of the rod is now 1.5 ft above the datum, you have

V_{g_2} = mgy = (30 lb)(1.5 ft) = 45 ft⋅lb

Kinetic Energy. Denote the angular velocity of the rod in position 2 by \omega_2. The rod rotates about O, so you have \bar{v}_2=\bar{r} \omega_2=1.5 \omega_2 and

\bar{I}=\frac{1}{12} m l^2=\frac{1}{12}\left(\frac{30~lb }{32.2~ft / s ^2}\right)(5~ft )^2=1.941~lb \cdot ft \cdot s ^2

T_2=\frac{1}{2} m \bar{v}_2^2+\frac{1}{2} \bar{I} \omega_2^2=\frac{1}{2} \frac{30}{32.2}\left(1.5 \omega_2\right)^2+\frac{1}{2}(1.941) \omega_2^2=2.019 \omega_2^2

Substituting these expressions into Eq. (1) give

0 + 0 + 75 ft·lb = 2.019\omega_2^2 + 45 ft·lb + 0          \omega_2 = 3.86 rad/s ↻ ◂

Reaction. Because \omega_2 = 3.86 rad/s, the components of the acceleration of G as the rod passes through position 2 are (Fig. 2)

\bar{a}_n=\bar{r} \omega_2^2=(1.5~ft )(3.86~rad / s )^2=22.3~ft / s ^2 \qquad \overline{ a }_n=22.3~ft / s ^2 \downarrow

\bar{a}_t=\bar{r} \alpha \qquad \qquad \qquad \qquad \overline{ a }_t=\bar{r} \alpha \rightarrow

Draw free-body and kinetic diagrams (Fig. 3) to express that the system of external forces is equivalent to the vector of components m \overline{ a }_t \text { and } m \overline{ a }_n attached at G and the couple \bar{I} \alpha.

+\circlearrowright \Sigma M_0=\bar{I} \alpha+m \bar{a} d_{\perp}: \qquad 0=\bar{I} \alpha+m(\bar{r} \alpha) \bar{r} \qquad \alpha=0

\stackrel{+}{\rightarrow} \Sigma F_x=m \bar{a}_x: \qquad R_x=m(\bar{r} \alpha) \qquad R_x=0

+\uparrow \Sigma F_y=m \bar{a}_y: \qquad \qquad R_y-30~lb =-m \bar{a}_n

R_y-30~lb =-\frac{30~lb }{32.2~ft / s ^2}\left(22.3~ft / s ^2\right)

R_y = +9.22 lb                   R_y = 9.22 lb ↑ ◂

REFLECT and THINK: This problem illustrates how you might need to supplement the conservation of energy with Newton’s second law. What if the spring constant had been smaller, say 180 lb/in.? You would have found V_{ e _1} = 7.5 ft⋅lb and then solved Eq. (1) to obtain \omega_2^2 = − 18.57 . This is clearly impossible and means that the rod would not make it to position 2 as assumed.