Question 3.SP.5: A cube of side a is acted upon by a force P along the diagon......

STRATEGY: Use the equations presented in this section to compute the moments asked for. You can find the distance between AG and FC from the expression for the moment M_{AG}

MODELING and ANALYSIS:
a. Moment about A. Choosing x, y, and z axes as shown (Fig. 1), resolve into rectangular components the force P and the vector \mathrm{r}_{F/A} = \overrightarrow{AF} drawn from A to the point of application F of P.

\begin{array}{l}{{\mathrm{r}_{F/A}=a\mathbf{i}-a\mathbf{j}=a(\mathbf{i}-\mathbf{j})}}\\ {{\mathrm{P}=(P/{\sqrt{2}})\mathbf{j}-(P/{\sqrt{2}})\mathbf{k}=(P/{\sqrt{2}})(\mathbf{j}-\mathbf{k})}}\end{array}

The moment of P about A is the vector product of these two vectors:

\mathbf{M}_{A}=\mathbf{r}_{F/ A}\times\mathbf{P}=a(\mathbf{i}-\mathbf{j})\times(P/\sqrt{2})(\mathbf{j}-\mathbf{k})

\mathbf{M}_{A}=(a P/{\sqrt{2}})(\mathbf{i}+\mathbf{j}+\mathbf{k})◂

b. Moment about AB. You want the projection of \mathbf{M}_{A} on AB:

M_{A B}=\mathbf{i}\cdot\mathbf{M}_{\mathrm{A}}=\mathbf{i}\cdot(a P/\sqrt2)(\mathbf{i}+\mathbf{j}+\mathbf{k})

M_{A B}=a P/{\sqrt{2}}◂

You can verify that because AB is parallel to the x axis, {M}_{AB} is also the x component of the moment \mathbf{M}_{A}

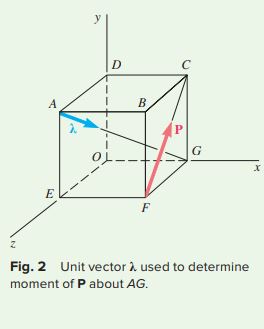
c. Moment about Diagonal AG. You obtain the moment of P about AG by projecting \mathbf{M}_{A} on AG. If you denote the unit vector along AG by λ (Fig. 2), the calculation looks like this:

\lambda={\frac{{\overrightarrow{{A G}}}}{A G}}={\frac{a\mathbf{i}-a\mathbf{j}-a\mathbf{k}}{a{\sqrt{3}}}}=(1/{\sqrt{3}})(\mathbf{i}-\mathbf{j}-\mathbf{k})

M_{A G}=\lambda\cdot{\bf M}_{A}=(1/\sqrt{3})(\bf i-j-k)\cdot(a P/\sqrt{2})(\bf \mathrm{i}+\mathrm{j}+\mathrm{k})

M_{A G}=(a P/\sqrt{6})(1-1-1)\,\,\,\,\,\,\,\,\,\,\,\,\,M_{A G}=-a P/\sqrt{6}◂

Alternative Method. You can also calculate the moment of P about AG from the determinant form:

M_{A/G}= \Bigg|\begin{array}{c c c} \lambda_{x}\;\; \lambda_{y}\;\; \lambda_{z} \\ x_{F/A}\; y_{F/A}\;z_{F/A} \\ F_{x}\;\; F_{y}\;\; F_{z} \end{array}\Bigg| =\Bigg|\begin{array}{c c c}{{1/\sqrt{3}}}&{{-1/\sqrt{3}}}&{{-1/\sqrt{3}}}\\ {{a}}&{{-a}}&{{0}}\\ {{0}}&{{P/\sqrt{2}}}&{{-P/\sqrt{2}}}\end{array}\Bigg|=aP/\sqrt{6}

d. Perpendicular Distance between AG and FC. First note that P is perpendicular to the diagonal AG. You can check this by forming the scalar product P · λ and verifying that it is zero:

\mathbf{P}\cdot\mathbf{\boldsymbol{\lambda}}=(P/{\sqrt{2}})(\mathbf{j}-\mathbf{k})\cdot(1/{\sqrt{3}})(\mathbf{i}-\mathbf{j}-\mathbf{k})=(P{\sqrt{6}})(0-1+1)=0

You can then express the moment {M}_{AG} as −Pd, where d is the perpendicular distance from AG to FC (Fig. 3). (The negative sign is needed because the rotation imparted to the cube by P appears as clockwise to an observer at G.) Using the value found for {M}_{AG} in part c,

M_{A G}=-P d=-a P/\sqrt{6}\qquad\qquad\qquad d=a/\sqrt{6}◂

REFLECT and THINK: In a problem like this, it is important to visualize the forces and moments in three dimensions so you can choose the appropriate equations for finding them and also recognize the geometric relationships between them.