Question 12.SP.13: A space tug travels a circular orbit with a 6000-mi radius a......
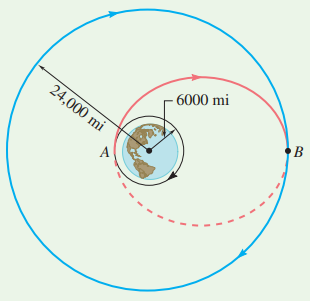
A space tug travels a circular orbit with a 6000-mi radius around the earth. In order to transfer it to a larger orbit with a 24,000-mi radius, the tug is first placed on an elliptical path AB by firing its engines as it passes through A, thus increasing its velocity by 3810 mi/h. Determine how much the tug’s velocity should be increased as it reaches B to insert it into the larger circular orbit.
Learn more on how we answer questions.
STRATEGY: Use Newton’s second law and conservation of angular momentum.
MODELING: Choose the space tug as the system, and assume you can treat it as a particle. Draw free-body and kinetic diagrams of the system at A as shown in Fig. 1.
ANALYSIS:
Circular Orbit through A. Applying Newton’s second law in the normal direction when the tug is at A gives
\begin{array}{c c}\underrightarrow{+}{{\Sigma F_{n}=m a_{n}}}\end{array}\qquad\qquad\qquad\frac{G M m}{r_{A}^{2}}=\frac{m\nu_{A}^{2}}{r_{A}}\qquad (1)Solve Eq. (1) for v_{A}, use Eq. 12.28, and substitute in numbers to find
GM = gR² (12.28)
v_{A}={\sqrt{\frac{G M}{r_{A}}}}={\sqrt{\frac{g R^{2}}{r_{A}}}}={\sqrt{\frac{(32.2{\mathrm{~ft}}/{s}^{2})((3960{\mathrm{~mi}})(5280{\mathrm{~ft}}/{\mathrm{mi}}))^{2}}{(600{\mathrm{~mi}})(5280{\mathrm{~ft}}/{\mathrm{mi}})}}}=21{\mathrm{,080~ft/s}}Converting this to mi/h gives v_{A} = 14,370 mi/h. Thus, the increased velocity to put the space tug into an elliptic orbit is (v_{A})_{ell} = 14,370 mi/h + 3810 mi/h = 18,180 mi/h.
Elliptical Path AB. To find the velocity at B, use the conservation of angular momentum between A and B. The velocity is perpendicular to r at both A and B, so you have
H_{O}=r_{A}m\nu_{A}=r_{B}m\nu_{B} (2)
Solving Eq. (2) for v_{B} and substituting in numbers give
(v_{B})_{\mathrm{ell}}=\frac{r_{A}}{r_{B}}(\nu_{A})_{\mathrm{ell}}=\frac{6000\mathrm{~mi}}{24,000\mathrm{~mi}}(18,180\mathrm{~mi}/h)=4545\ \mathrm{mi}/h
Circular Orbit through B. Applying Newton’s second law in the normal direction when the tug is at B gives
\underleftarrow{+}\Sigma F_{n}=m a_{n}\qquad\qquad\qquad {\frac{G M m}{r_{B}^{2}}}={\frac{m\nu_{B}^{2}}{r_{B}}} (3)
By solving Eq. (3) for v_{B} and substituting in numbers, you find
v_{B}={\sqrt{\frac{G M}{r_{B}}}}={\sqrt{\frac{g R^{2}}{r_{B}}}}={\sqrt{\frac{(32.2~\mathrm{ft/{s}}^{2})((3960~\mathrm{{mi}})(5280~\mathrm{{ft}}/{\mathrm{{mi}}}))^{2}}{(24,000~\mathrm{{mi}})(5280~\mathrm{{ft}}/{\mathrm{{mi}}})}}}= 10,540 ft/s
This is the speed of the space tug at B for it to have a circular orbit. Converting this to mi/h gives v_{B} = 7186 mi/h. Therefore, the required increase in velocity is
\Delta v_{B} = 7186 mi/h − 4545 mi/h
\Delta v_{B} = 2640 mi/h ◂
REFLECT and THINK: The speeds of satellites and orbiting vehicles are quite large, as seen in this problem. The next type of question we could ask is what force is required to impart this change in speed.
