Question 9.SP.14: Consider a rectangular prism with a mass of m and sides a, b......
Consider a rectangular prism with a mass of m and sides a, b, and c. Determine (a) the moments and products of inertia of the prism with respect to the coordinate axes shown, (b) its moment of inertia with respect to the diagonal OB.
STRATEGY: For part (a), you can introduce centroidal axes and apply the parallel-axis theorem. For part (b), determine the direction cosines of line OB from the given geometry and use either Eq. (9.46) or (9.50).
I_{O L}=I_x \lambda_x^2+I_y \lambda_y^2+I_z \lambda_z^2-2 I_{x y} \lambda_x \lambda_y-2 I_{y z} \lambda_y \lambda_z-2 I_{z x} \lambda_z \lambda_x (9.46)
I_{O L}=I_{x^{\prime}} \lambda_{x^{\prime}}^2+I_{y^{\prime}} \lambda_{y^{\prime}}^2+I_{z^{\prime}} \lambda_{z^{\prime}}^2 (9.50)

Learn more on how we answer questions.
MODELING and ANALYSIS: a. Moments and Products of Inertia with Respect to the Coordinate Axes.
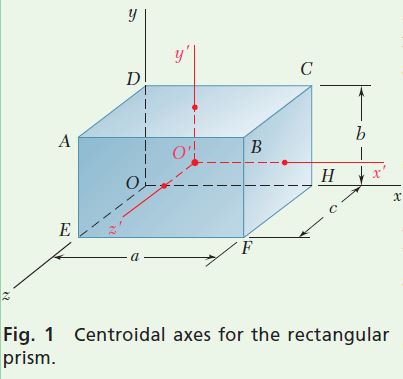
Moments of Inertia. Introduce the centroidal axes x’, y’, and z’ with respect to which the moments of inertia are given in Fig. 9.28, and then apply the parallel-axis theorem (Fig. 1). Thus,
I_x=\bar{I}_{x^{\prime}}+m\left(\bar{y}^2+\bar{z}^2\right)=\frac{1}{12} m\left(b^2+c^2\right)+m\left(\frac{1}{4} b^2+\frac{1}{4} c^2\right)
I_x=\frac{1}{3} m\left(b^2+c^2\right)
Similarly,
I_y=\frac{1}{3} m\left(c^2+a^2\right) \quad I_z=\frac{1}{3} m\left(a^2+b^2\right)
Products of Inertia. Because of symmetry, the products of inertia with respect to the centroidal axes x’, y’, and z’ are zero, and these axes are principal axes of inertia. Using the parallel-axis theorem, you have
I_{x y}=\bar{I}_{x^{\prime} y^{\prime}}+m \bar{x} \bar{y}=0+m\left(\frac{1}{2} a\right)\left(\frac{1}{2} b\right) \quad I_{x y}=\frac{1}{4} m a b
Similarly,
I_{y z}=\frac{1}{4} m b c \quad I_{z x}=\frac{1}{4} m c a
b. Moment of Inertia with Respect to OB. Recall Eq. (9.46):
I_{O B}=I_x \lambda_x^2+I_y \lambda_y^2+I_z \lambda_z^2-2 I_{x y} \lambda_x \lambda_y-2 I_{y z} \lambda_y \lambda_z-2 I_{z x} \lambda_z \lambda_x
where the direction cosines of OB are (Fig. 2)
\lambda_x=\cos \theta_x=\frac{O H}{O B}=\frac{a}{\left(a^2+b^2+c^2\right)^{1 / 2}}
\lambda_y=\frac{b}{\left(a^2+b^2+c^2\right)^{1 / 2}} \quad \lambda_z=\frac{c}{\left(a^2+b^2+c^2\right)^{1 / 2}}
Substituting the values obtained in part (a) for the moments and products of inertia and for the direction cosines into the equation for I_{O B}, you obtain
\begin{array}{r}I_{O B}=\frac{1}{a^2+b^2+c^2}\left[\frac{1}{3} m\left(b^2+c^2\right) a^2+\frac{1}{3} m\left(c^2+a^2\right) b^2+\frac{1}{3} m\left(a^2+b^2\right) c^2\right. \\\left.-\frac{1}{2} m a^2 b^2-\frac{1}{2} m b^2 c^2-\frac{1}{2} m c^2 a^2\right]\end{array}
I_{O B}=\frac{m}{6} \frac{a^2 b^2+b^2 c^2+c^2 a^2}{a^2+b^2+c^2}
REFLECT and THINK: You can also obtain the moment of inertia I_{O B} directly from the principal moments of inertia \bar{I}_{x^{\prime}}, \bar{I}_{y^{\prime}}, \text { and } \bar{I}_{z^{\prime}}, since the line OB passes through the centroid O’. Since the x’, y’, and z’ axes are principal axes of inertia (Fig. 3), use Eq. (9.50) to write
\begin{aligned}I_{O B} & =\bar{I}_{x^{\prime}} \lambda_x^2+\bar{I}_{y^{\prime}} \lambda_y^2+\bar{I}_{z^{\prime}} \lambda_z^2 \\& =\frac{1}{a^2+b^2+c^2}\left[\frac{m}{12}\left(b^2+c^2\right) a^2+\frac{m}{12}\left(c^2+a^2\right) b^2+\frac{m}{12}\left(a^2+b^2\right) c^2\right]\end{aligned}
I_{O B}=\frac{m}{6} \frac{a^2 b^2+b^2 c^2+c^2 a^2}{a^2+b^2+c^2}