Construct a triangle knowing a side, the perimeter, and the area (construct the figure formed by the inscribed circle and an escribed circle). Among all triangles with a given side and given area, which has the smallest perimeter? Among all triangles with a given side and given perimeter, which has

Question

Construct a triangle knowing a side, the perimeter, and the area (construct the figure formed by the inscribed circle and an escribed circle). Among all triangles with a given side and given area, which has the smallest perimeter? Among all triangles with a given side and given perimeter, which has the largest area?

Accepted Answer

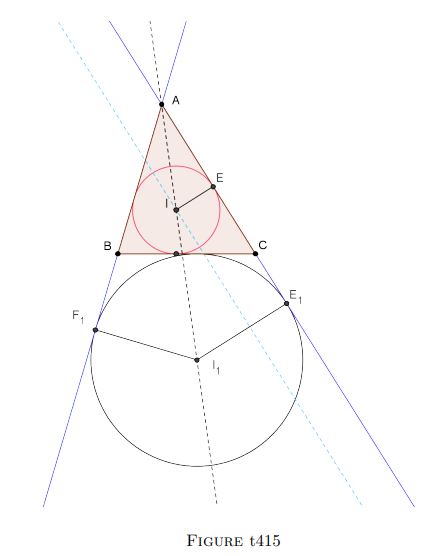
The solution to this problem is only slightly different from the solu-tion to exercise 415, so we will use the same diagram (fig. t415). In that diagram, suppose ABC is the required triangle. We are given BC = a, the perimeter of ABC, which we will denote as 2s, and its area k. Suppose I is the incenter of ABC, r its radius, and E its point of tangency with side AC. Further, let [latex]I_{1}[/latex] be the excenter opposite vertex A, let [latex]r_{1}[/latex] be the radius of the corresponding escribed circle, and let [latex]E_{1}[/latex] be the point of contact of the escribed circle with side AC (extended). From the result of exercise 90b, we have AE = s − a, and [latex]E E_{1}=A E_{1}-A E=[/latex] s − (s − a) = a. From the result of exercise 299, we have:

(1) [latex]r={\frac{k}{s}};\;\;\;\;\;\;\;\;\;\;\;r_{1}={\frac{k}{s-a}}.[/latex]

Thus we can construct point [latex]E_{1},[/latex] then segment [latex]E E_{1}=a,[/latex] then the radii [latex] r_{1},\;r_{1}[/latex] (but see the note to exercise 415), and finally circles [latex]I,\ I_{1}[/latex] (the inscribed and escribed circles of the triangle). The construction is completed by drawing the common internal tangent of the two circles, and another common external tangent.

Next we investigate the possibility of performing the construction. We need circles [latex]I,\ I_{1}[/latex] to be outside each other, or at worst tangent to each other. That is, we need [latex]I_{1}{I}^{2}=a^{2}+(r_{1}-r)^{2}\geq(r_{1}+r)^{2},[/latex] which simplifies to [latex]a^{2}\geq4r r_{1}.[/latex]

We now determine the triangle with smallest perimeter, among those with a given side and area. For given values of a and k the equations (1) above show that radii [latex]r,r_{1}[/latex] both increase as s decreases. The smallest perimeter thus corresponds to the extreme situation where [latex]a^{2}=4r r_{1};[/latex] that is, when [latex]I I_{1}=r+r_{1}.[/latex] This means that triangle ABC will be isosceles.

Finally, we look at the question of finding the triangle with largest area, if a side and the perimeter are fixed. We again use (1) to note that if a and s are fixed, then r and [latex]r_{1}[/latex] increase as k increases. So the largest value of k corresponds to the same situation, when [latex]a^{2}=4r r_{1},[/latex] which is again when ABC is isosceles.

Notes (i). We are not given [latex]r,\ r_{1};[/latex] students can use (1) to rephrase this condition for existence of triangle ABC in terms of the quantities which are given.

(ii). We can also find the triangle of largest area of those with a given perimeter and given side by using the results of 251. The formula derived there can be written as [latex]k^{2}={ extstyle{\frac{1}{4}}}s(s-a)[a^{2}-(b-c)^{2}].[/latex] Thus for fixed s and a, the area will increase as |b − c| decreases. Thus the area will be largest when b = c.

(iii). We can use another argument to find the triangle of smallest perimeter, when the area k and a side a are fixed. Suppose ∆ is an isosceles triangle with area k, perimeter 2s, and base a. Suppose [latex]\Delta^{\prime}[/latex] is any non-isosceles triangle with area k, perimeter [latex]2s^{\prime}.[/latex] , and base a. We will show that [latex]s\lt s^{\prime}.[/latex]

Indeed, we can construct isosceles triangle [latex]\Delta_{1}[/latex] with base a and perimeter [latex]2s^{\prime},[/latex] and let [latex]k_{1}[/latex] be its area. We then compare triangles [latex]\Delta^{\prime}[/latex] and [latex]\Delta_{1}[/latex]. They have the same base, and the same perimeter [latex]2s^{\prime},[/latex] so from result (ii) above we know that [latex]k_1 > k.[/latex]

Let h be the common altitude to side a of [latex]∆, \Delta^{\prime},[/latex] and let [latex]h_1[/latex] be the corresponding altitude of [latex]\Delta_{1}[/latex] Then [latex] h_1 > h,[/latex] and comparing triangles [latex]∆, \Delta_{1}[/latex], it follows that [latex]s^{\prime}\gt s.[/latex] (We use the fact that the larger projection corresponds to the larger declination, so that in isosceles triangles with equal bases the larger altitude corresponds to the larger leg.)

Question P.416: Construct a triangle knowing a side, the perimeter, and the ......

This Question has been Answered.

Already have an account?

Login

Related Answered Questions

Verified Answer:

The radii of the circles circumscribing (Exercise 66) the quadrilaterals determined by the bisectors of the interior (or exterior) angles of a quadrilat-eral are in the ratio a+c-b-d/a+c+b+d, where a, b, c, d are the sides of the given quadrilateral, taken in their natural order. ...

Verified Answer:

Verified Answer:

Verified Answer:

Construct a cyclic quadrilateral knowing its sides. ...

Verified Answer:

Construct a triangle knowing an angle, the perimeter, and the area (Exercises 90b, 299). Among all triangles with a given angle and given perimeter, which one has largest area? ...

Verified Answer:

Another solution to Exercise 329: to draw through a given point inside an angle a secant which forms, with the sides of the angle, a triangle with given area. Construct first the parallelogram with a vertex at the given point, and two sides on the sides of the angle. This parallelogram cuts from ...

Verified Answer:

Verified Answer:

We are given two parallel lines, and a common perpendicular which intersects them in A, B. Points C, D are taken on these lines so that trape-zoid ABCD has an area equal to that of a given square. Let H be the projection on CD of the midpoint of AB. Find the locus of H. (One must distinguish two ...

Verified Answer:

Verified Answer: