Question 6.SP.5: Determine the components of the forces acting on each member......
Determine the components of the forces acting on each member of the frame shown.

Learn more on how we answer questions.
STRATEGY: The approach to this analysis is to consider the entire frame as a free body to determine the reactions, and then consider separate members. However, in this case, you will not be able to determine forces on one member without analyzing a second member at the same time.
MODELING and ANALYSIS: The external reactions involve only three
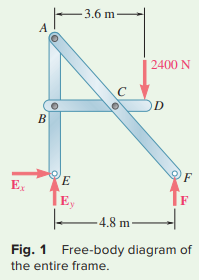
unknowns, so compute the reactions by considering the free-body diagram of the entire frame (Fig. 1).
+↺ΣM_{E} = 0: − (2400 N)(3.6 m) + F(4.8 m) = 0
F = +1800 N F = 1800 N↑ ◂
+↑ΣF_{y} = 0: − 2400 N + 1800 N + E_{y}= 0
E_{y} = +600 N E_{y} = 600 N↑ ◂
\underrightarrow{+}\Sigma F_{x}=0\colon
\mathrm{E}_{x}=0 ◂
Now dismember the frame. Because only two members are connected at each joint, force components are equal and opposite on each member at each joint (Fig. 2).
Free Body: Member BCD.
+↺\begin{array}{r l r l}{{\Sigma M_{B}=0\colon\quad}}&{{\ {\displaystyle-(2400\,\mathrm{N})(3.6~m)+C_{y}(2.4~m)=0}}}&{{\qquad C_{y}=+3600\,\mathrm{N}}}\end{array} ◂
+↺\begin{array}{r l r l}{{\Sigma M_{C}=0\colon\;\;\;}}&{{~-(2400\,{ N})(1.2\,{ m})+B_{y}(2.4\,{ m})=0}}&{{~~~~B_{y}=+1200\,{ N}}}\end{array} ◂
\begin{array}{c c}{{\underrightarrow{+}\Sigma F_{x}=0\colon}}&{{\qquad-B_{x}+C_{x}=0}}\end{array}
Neither B_{x}~nor~C_{x} can be obtained by considering only member BCD; you need to look at member ABE. The positive values obtained for B_{y}~and~C_{y} indicate that the force components B_{y}~and~C_{y} are directed as assumed.
Free Body: Member ABE.
+↺\Sigma M_{A}=0\colon\qquad\qquad\qquad\qquad B_{x}(2.7\,\mathrm{m})=0\qquad\qquad\qquad\qquad\qquad B_{x}=0 ◂
\underrightarrow{+}\Sigma F_{x} = 0\colon \qquad\qquad\qquad\qquad +B_{x} – A_{x} = 0 \qquad\qquad\qquad\qquad\qquad A_{x} = 0 ◂
+↑ΣF_{y} = 0\colon \qquad\qquad\qquad\qquad -A_{y} + B_{y} + 600~\mathrm{N} = 0
-A_{y} + 1200~\mathrm{N} + 600~\mathrm{N} = 0 \qquad\qquad A_{y} = + 1800~\mathrm{N} ◂
Free Body: Member BCD. Returning now to member BCD, you have
\underrightarrow{+}\Sigma F_{x} = 0\colon \qquad\qquad -B_{x} + C_{x} = 0 \qquad 0 + C_{x} = 0 \qquad\qquad C_{x} = 0 ◂
REFLECT and THINK: All unknown components have now been found. To check the results, you can verify that member ACF is in equilibrium.
+↺\Sigma M_{C}=(1800\:\mathrm{N})(2.4\,\mathrm{m})-A_{y}(2.4\,\mathrm{m})-A_{x}(2.7\,\mathrm{m})
\qquad\qquad= (1800 N)(2.4 m) − (1800 N)(2.4 m) − 0 = 0 (checks)