Question 9.SP.8: For the section shown, the moments and product of inertia wi......
For the section shown, the moments and product of inertia with respect to the x and y axes are
I_x=7.20 \times 10^6 \mathrm{~mm}^4 \quad I_y=2.59 \times 10^6 \mathrm{~mm}^4 \quad I_{x y}=-2.54 \times 10^6 \mathrm{~mm}^4
Using Mohr’s circle, determine (a) the principal axes of the section about O, (b) the values of the principal moments of inertia of the section about O, and (c) the moments and product of inertia of the section with respect to the x’ and y’ axes that form an angle of 60° with the x and y axes.
STRATEGY: You should carefully draw Mohr’s circle and use the geometry of the circle to determine the orientation of the principal axes. Then complete the analysis for the requested moments of inertia.

Learn more on how we answer questions.
MODELING:
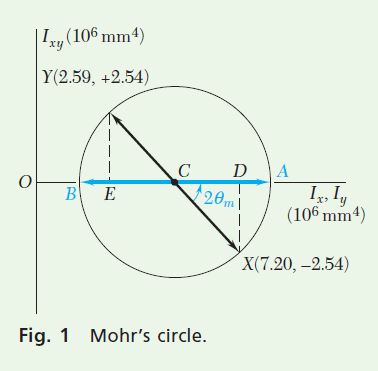
Drawing Mohr’s Circle. First plot point X with coordinates I_x=7.20, I_{x y}=-2.54, and plot point Y with coordinates I_y=2.59, -I_{x y}=+2.54. Join X and Y with a straight line to define the center C of Mohr’s circle (Fig. 1). You can measure the abscissa of C, which represents I_{\mathrm{ave}}, and the radius R of the circle either directly or using
I_{\mathrm{ave}}=O C=\frac{1}{2}\left(I_x+I_y\right)=\frac{1}{2}\left(7.20 \times 10^6+2.59 \times 10^6\right)=4.895 \times 10^6 \mathrm{~mm}^4
C D=\frac{1}{2}\left(I_x-I_y\right)=\frac{1}{2}\left(7.20 \times 10^6-2.59 \times 10^6\right)=2.305 \times 10^6 \mathrm{~mm}^4
R=\sqrt{(C D)^2+(D X)^2}=\sqrt{\left(2.305 \times 10^6\right)^2+\left(2.54 \times 10^6\right)^2}
=3.430 \times 10^6 \mathrm{~mm}^4
ANALYSIS:
a. Principal Axes. The principal axes of the section correspond to points A and B on Mohr’s circle, and the angle through which you should rotate CX to bring it into CA defines 2 \theta_m. You obtain
\tan 2 \theta_m=\frac{D X}{C D}=\frac{2.54}{2.305}=1.102 \quad 2 \theta_m=47.8^{\circ} ↺ \theta_m=23.9^{\circ} ↺
Thus, the principal axis Oa corresponding to the maximum value of the moment of inertia is obtained by rotating the x axis through 23.9° counterclockwise; the principal axis Ob corresponding to the minimum value of the moment of inertia can be obtained by rotating the y axis through the same angle (Fig. 2).
b. Principal Moments of Inertia. The principal moments of inertia are represented by the abscissas of A and B. The results are
I_{\max }=O A=O C+C A=I_{\mathrm{ave}}+R=(4.895+3.430) 10^6 \mathrm{~mm}^4
I_{\max }=8.33 \times 10^6 \mathrm{~mm}^4
I_{\min }=O B=O C-B C=I_{\mathrm{ave}}-R=(4.895-3.430) 10^6 \mathrm{~mm}^4
I_{\min }=1.47 \times 10^6 \mathrm{~mm}^4
c. Moments and Product of Inertia with Respect to the x’ and y’ Axes. On Mohr’s circle, you obtain the points X’ and Y’, which correspond to the x’ and y’ axes, by rotating CX and CY through an angle 2θ = 2(60°) = 120° counterclockwise (Fig. 3). The coordinates of X’ and Y’ yield the desired moments and product of inertia. Noting that the angle that CX’ forms with the horizontal axis is \phi=120^{\circ} – 47.8° = 72.2°, you have
I_{x^{\prime}}=O F=O C+C F=4.895 \times 10^6 \mathrm{~mm}^4+\left(3.430 \times 10^6 \mathrm{~mm}^4\right) \cos 72.2^{\circ}
I_{x^{\prime}}=5.94 \times 10^6 \mathrm{~mm}^4
I_{y^{\prime}}=O G=O C-G C=4.895 \times 10^6 \mathrm{~mm}^4-\left(3.430 \times 10^6 \mathrm{~mm}^4\right) \cos 72.2^{\circ}
I_{y^{\prime}}=3.85 \times 10^6 \mathrm{~mm}^4
I_{x^{\prime} y^{\prime}}=F X^{\prime}=\left(3.430 \times 10^6 \mathrm{~mm}^4\right) \sin 72.2^{\circ}
I_{x^{\prime} y^{\prime}}=3.27 \times 10^6 \mathrm{~mm}^4
REFLECT and THINK: This problem illustrates typical calculations with Mohr’s circle. The technique is a useful one to learn and remember.