Question 3.SP.9: Four tugboats are bringing an ocean liner to its pier. Each ......
Four tugboats are bringing an ocean liner to its pier. Each tugboat exerts a 5000-lb force in the direction shown. Determine (a) the equivalent forcecouple system at the foremast O, (b) the point on the hull where a single, more powerful tugboat should push to produce the same effect as the original four tugboats.
STRATEGY: The equivalent force-couple system is defined by the sum of the given forces and the sum of the moments of those forces at a particular point. A single tugboat could produce this system by exerting the resultant force at a point of application that produces an equivalent moment.

Learn more on how we answer questions.
Final Answer
MODELING and ANALYSIS:
a. Force-Couple System at O. Resolve each of the given forces into components, as in Fig. 1 (kip units are used). The force-couple system at O equivalent to the given system of forces consists of a force R and a couple \mathbf{M}_O^R defined as
\begin{aligned}\mathbf{R} & =\Sigma \mathbf{F} \\& =(2.50 \mathbf{i}-4.33 \mathbf{j})+(3.00 \mathbf{i}-4.00 \mathbf{j})+(-5.00 \mathbf{j})+(3.54 \mathbf{i}+3.54 \mathbf{j}) \\& =9.04 \mathbf{i}-9.79 \mathbf{j}\end{aligned}
\begin{aligned}\mathbf{M}_O^R= & \Sigma(\mathbf{r} \times \mathbf{F}) \\= & (-90 \mathbf{i}+50 \mathbf{j}) \times(2.50 \mathbf{i}-4.33 \mathbf{j}) \\& +(100 \mathbf{i}+70 \mathbf{j}) \times(3.00 \mathbf{i}-4.00 \mathbf{j}) \\& +(400 \mathbf{i}+70 \mathbf{j}) \times(-5.00 \mathbf{j}) \\& +(300 \mathbf{i}-70 \mathbf{j}) \times(3.54 \mathbf{i}+3.54 \mathbf{j}) \\= & (390-125-400-210-2000+1062+248) \mathbf{k} \\= & -1035 \mathbf{k}\end{aligned}
The equivalent force-couple system at O is thus (Fig. 2)
\mathbf{R}=(9.04 ~\mathrm{kips}) \mathbf{i}-(9.79 ~\mathrm{kips}) \mathbf{j} \quad \mathbf{M}_O^R=-(1035 ~\mathrm{kip} \cdot \mathrm{ft}) \mathbf{k}
or
\mathbf{R}=13.33 ~\mathrm{kips} \angle47.3^{\circ} \quad \mathbf{M}_O^R=1035 ~\mathrm{kip} \cdot \mathrm{ft}
Remark: Since all the forces are contained in the plane of the figure, you would expect the sum of their moments to be perpendicular to that plane. Note that you could obtain the moment of each force component directly from the diagram by first forming the product of its magnitude and perpendicular distance to O and then assigning to this product a positive or a negative sign, depending upon the sense of the moment.
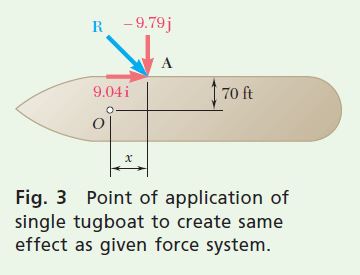
b. Single Tugboat. The force exerted by a single tugboat must be equal to R, and its point of application A must be such that the moment of R about O is equal to \mathbf{M}_O^R (Fig. 3). Observing that the position vector of A is
\mathbf{r}=x \mathbf{i}+70 \mathbf{j}
you have
\begin{aligned}\mathbf{r} \times \mathbf{R} & =\mathbf{M}_O^R \\(x \mathbf{i}+70 \mathbf{j}) \times(9.04 \mathbf{i}-9.79 \mathbf{j}) & =-1035 \mathbf{k} \\-x(9.79) \mathbf{k}-633 \mathbf{k} & =-1035 \mathbf{k} \quad x=41.1 ~\mathrm{ft}\end{aligned}
REFLECT and THINK: Reducing the given situation to that of a single force makes it easier to visualize the overall effect of the tugboats in maneuvering the ocean liner. But in practical terms, having four boats applying force allows for greater control in slowing and turning a large ship in a crowded harbor.