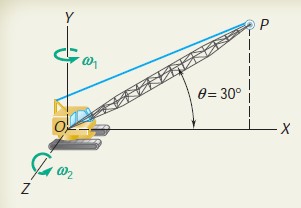
Question 15.11: The crane shown rotates with a constant angular velocity V1 ......
The crane shown rotates with a constant angular velocity \text V_1 of 0.30 rad/s. Simultaneously, the boom is being raised with a constant angular velocity \text V_2 of 0.50 rad/s relative to the cab. Knowing that the length of the boom OP is l = 12 m, determine (a) the angular velocity V of the boom, (b) the angular acceleration A of the boom, (c) the velocity v of the tip of the boom, (d) the acceleration a of the tip of the boom.
a. Angular Velocity of Boom. Adding the angular velocity \text V_1 of the cab and the angular velocity \text V_2 of the boom relative to the cab, we obtain the angular velocity V of the boom at the instant considered:
\mathrm{V}=\mathrm{V}_{1}+\mathrm{V}_{2} \quad\quad\quad \mathrm{V}=(0.30 ~\mathrm{rad} / \mathrm{s}) {j}+(0.50~ \mathrm{rad} / \mathrm{s}){k}b. Angular Acceleration of Boom. The angular acceleration A of the boom is obtained by differentiating V. Since the vector \text V_1 is constant in magnitude and direction, we have
\mathrm{A}=\mathrm{\dot V}=\mathrm{\dot V}_{1}+\mathrm{\dot V}_{2}=0+\mathrm{\dot V}_{2}where the rate of change \mathrm{\dot V}_2 is to be computed with respect to the fixed frame OXYZ. However, it is more convenient to use a frame Oxyz attached to the cab and rotating with it, since the vector \text V_2 also rotates with the cab and therefore has zero rate of change with respect to that frame. Using Eq. (15.31) with Q = \text V_2 and Ω = \text V_1, we write
A = (0.15 rad/s²)i
c. Velocity of Tip of Boom. Noting that the position vector of point P is r = (10.39 m)i + (6 m)j and using the expression found for V in part a, we write
\begin{aligned}\mathrm{v}=\mathrm{V} \times {r}=\left|\begin{array}{ccc}{i} & {j} & {k} \\0 & 0.30~ \mathrm{rad} / \mathrm{s} & 0.50 ~\mathrm{rad} / \mathrm{s} \\10.39 \mathrm{~m} & 6 \mathrm{~m} & 0\end{array}\right| \\\mathrm{v}=-(3 \mathrm{~m} / \mathrm{s}){i}+(5.20 \mathrm{~m} / \mathrm{s}){j}-(3.12 \mathrm{~m} / \mathrm{s}){k}\end{aligned}d. Acceleration of Tip of Boom. Recalling that v = V × r, we write
