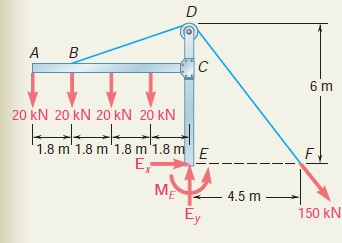
Question 4.4: The frame shown supports part of the roof of a small buildin......
The frame shown supports part of the roof of a small building. Knowing that the tension in the cable is 150 kN, determine the reaction at the fixed end E.

The blue check mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
Free-Body Diagram. A free-body diagram of the frame and of the cable BDF is drawn. The reaction at the fixed end E is represented by the force components {E}_{x}\operatorname{and}\ {E}_{y} and the couple {M}_{E}. The other forces acting on the free body are the four 20-kN loads and the 150-kN force exerted at end F of the cable.
Equilibrium Equations. Noting that DF~=~2\overline{(4.5~m)^2~ + ~(6~m)^2} ~=~7.5~m, we write
\stackrel{+}{\to}\Sigma F_{x}\;=\;0\mathrm{:}\qquad\qquad\qquad E_{x}+{\frac{4.5}{7.5}}(150\,\mathrm{kN})\,=\,0 \\ \\ \qquad\qquad\qquad\qquad\qquad\qquad E_{x}=-90.0\,\mathrm{kN}\qquad\qquad\mathrm{E}_{x}=90.0\mathrm{kN}\,Z+\uparrow\Sigma F_{y}\,=\,0\mathrm{:}\qquad\qquad\qquad E_{y}-4(20\,\mathrm{kN})\,-\,\frac6{7.5}(150\,\mathrm{kN})\,=\,0 \\ \\ \qquad\qquad\qquad\qquad\qquad\qquad E_{y}=\ +200\mathrm{~kN}\qquad\qquad\ \ \ E_{y}=\ 200\mathrm{~kN}~X
+{\mathrm l{{\Sigma}}M_{E}=0}\mathrm{:}\qquad\qquad\qquad (20\mathrm{~kN})(7.2\mathrm{~m})\,+\,(20\mathrm{~kN})(5.4\mathrm{~m})\,+\,(20\mathrm{~kN})(3.6\mathrm{~m}) \\ \\ \qquad\qquad\qquad +~(20~\mathrm{kN})(1.8~\mathrm{m})-\frac{6}{7.5}(150~\mathrm{kN})(4.5~\mathrm{m})\,+\,M_{E}\,=\,0 \\ \\ \qquad\qquad\qquad\qquad\qquad\qquad M_{E}=+180.0\,\,\mathrm{kN}\cdot\,\mathrm{m}\qquad\mathrm{M}_{E}=\,180.0\,\,\mathrm{kN}\cdot\,\mathrm{m}\,\,1
Loading more images...
Related Answered Questions
Question: 4.5
Verified Answer:
Free-Body Diagram. We draw a free-body diagram of ...
Question: 4.3
Verified Answer:
Free-Body Diagram. A free-body diagram of the car ...
Question: 4.2
Verified Answer:
Free-Body Diagram. A free-body diagram of the beam...
Question: 4.10
Verified Answer:
Free-Body Diagram. The free-body diagram of the pi...
Question: 4.7
Verified Answer:
Free-Body Diagram. A free-body diagram of the ladd...
Question: 4.9
Verified Answer:
Free-Body Diagram. A free-body diagram is drawn wi...
Question: 4.8
Verified Answer:
Free-Body Diagram. A free-body diagram of the sign...
Question: 4.6
Verified Answer:
Free-Body Diagram. The joist is a three-force body...
Question: 4.SP.1
Verified Answer:
STRATEGY: Draw a free-body diagram to show all of ...