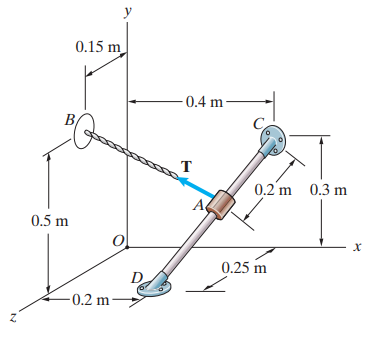
Question 2.138: The rope AB exerts a 50-N force T on the collar at A. Let rC......
The rope AB exerts a 50-N force T on the collar at A. Let r_{CA} be the position vector from point C to point A. Determine the cross product r_{CA} × T.
The rope AB exerts a 50-N force T on the collar at A.
The position vector from point C to point A is denoted as r_CA.
Step 1:
In this problem, we are given the vectors r_CD, r_CA, r_OB, and r_OC, and we need to find the vector r_AB and the vector T.
Step 2:
To find r_AB, we subtract the vectors r_OC and r_CA from r_OB. This gives us the vector r_AB = r_OB - (r_OC + r_CA).
Step 3:
To find T, we multiply the vector r_AB by the scalar 50 N and divide it by the magnitude of r_AB. This gives us the vector T = (50 N) * (r_AB / |r_AB|).
Step 4:
Next, we are asked to find the cross product of r_CA and T, which is denoted as r_CA x T. The cross product of two vectors is a vector that is perpendicular to both vectors and its magnitude is given by the product of the magnitudes of the two vectors multiplied by the sine of the angle between them.
Step 5:
To find the cross product, we can use the determinant method. We write the vectors r_CA and T as rows in a 3x3 matrix, with the unit vectors i, j, and k as the first column. Taking the determinant of this matrix gives us the components of the cross product vector r_CA x T.
Step 6:
Finally, we can express the result as (-47.2 i - 3.48 j - 7.96 k) N - m, which represents the vector r_CA x T.
Final Answer
We define the appropriate vectors.
\begin{aligned}r _{C D} & =(-0.2 i -0.3 j +0.25 k )~m \\r _{C A} & =(0.2~m ) \frac{ r _{C D}}{\left| r _{C D}\right|}=(-0.091 i -0.137 j +0.114 k ) ~m \\r _{O B} & =(0.5 j +0.15 k )~m \\r _{O C} & =(0.4 i +0.3 j )~m \\r _{A B} & = r _{O B}-\left( r _{O C}+ r _{C A}\right)=(0.61 i -1.22 j -0.305 k )~m \\T & =(50~N ) \frac{ r _{A B}}{\left| r _{A B}\right|}=(-33.7 i +36.7 j +3.93 k )~N\end{aligned}
Now take the cross product
\begin{aligned}&r _{C A} \times T =\left|\begin{array}{ccc} i & j & l \\-0.091 & -0.137 & 0.114 \\-33.7 & 36.7 & 3.93\end{array}\right|=(-4.72 i -3.48 j +-7.96 k )~N – m\\\\&r _{C A} \times T =(-47.2 i -3.48 j +-7.96 k )~N – m\end{aligned}
Related Answered Questions
Question: 2.163
Verified Answer:
The strategy is to expand the forces into scalar c...
Question: 2.166
Verified Answer:
From Problem 2.165 we know that
T = (333i + 333j -...
Question: 2.165
Verified Answer:
We have
\begin{aligned}&r _{C E}=(0.2 i...
Question: 2.135
Verified Answer:
\begin{aligned}r _{O A} & =6 i -2 j +3 ...
Question: 2.134
Verified Answer:
The two radius vectors are
r _{O B}=4 i +4 ...
Question: 2.158
Verified Answer:
The strategy is to define the unit vector pointing...
Question: 2.159
Verified Answer:
The vector r is
r =| r |\left(\sin 45^{\cir...
Question: 2.145
Verified Answer:
One strategy is to expand the determinant in terms...
Question: 2.137
Verified Answer:
We have r _A=(6 i +8 j +4 k )~m , r _B=(8 i...
Question: 2.160
Verified Answer:
We can write the force as
F =| F |\left(\co...