Question 2.158: The rope exerts a force of magnitude |F| = 200 lb on the top......
The rope exerts a force of magnitude |F| = 200 lb on the top of the pole at B.
(a) Determine the vector r_{AB} × F, where r_{AB} is the position vector from A to B.
(b) Determine the vector r_{AC} × F, where r_{AC} is the position vector from A to C.
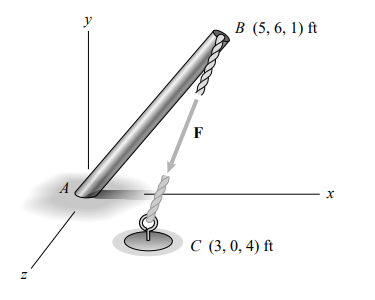
The rope exerts a force of magnitude |F| = 200 lb on the top of the pole at B.
Final Answer
The strategy is to define the unit vector pointing from B to A, express the force in terms of this unit vector, and take the cross product of the position vectors with this force. The position vectors
\begin{aligned}&r _{A B}=5 i +6 j +1 k , \quad r _{A C}=3 i +0 j +4 k\\&r _{B C}=(3-5) i +(0-6) j +(4-1) k =-2 i -6 j +3 k\end{aligned}
The magnitude \left| r _{B C}\right|=\sqrt{2^2+6^2+3^2}=7. The unit vector is
e _{B C}=\frac{ r _{B C}}{\left| r _{B C}\right|}=-0.2857 i -0.8571 j +0.4286 k.
The force vector is
F =| F | e _{B C}=200 e _{B C}=-57.14 i -171.42 j +85.72 k.
The cross products:
\begin{aligned}r _{A B} \times F & =\left|\begin{array}{ccc} i & j & k \\5 & 6 & 1 \\-57.14 & -171.42 & 85.72\end{array}\right| \\\\& =685.74 i -485.74 j -514.26 k \\\\& =685.7 i -485.7 j -514.3 k~( ft – lb )\end{aligned}
\begin{aligned}r _{A C} \times F & =\left|\begin{array}{ccc} i & j & k \\3 & 0 & 4 \\-57.14 & -171.42 & 85.72\end{array}\right| \\\\& =685.68 i -485.72 j -514.26 k \\\\& =685.7 i -485.7 j -514.3 k ~( ft – lb )\end{aligned}