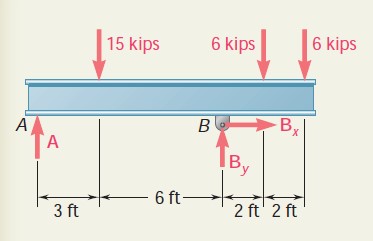
Question 4.2: Three loads are applied to a beam as shown. The beam is supp......
Three loads are applied to a beam as shown. The beam is supported by a roller at A and by a pin at B. Neglecting the weight of the beam, determine the reactions at A and B when P = 15 kips.

Learn more on how we answer questions.
Free-Body Diagram. A free-body diagram of the beam is drawn. The reaction at A is vertical and is denoted by A. The reaction at B is represented by components {B}_{x}\operatorname{and}\ {B}_{y}. Each component is assumed to act in the direction shown.
Equilibrium Equations. We write the following three equilibrium equations and solve for the reactions indicated:
\stackrel{+}{\rightarrow}\Sigma F_{x}=0:\qquad\qquad\qquad\qquad B_{x}=0 \qquad\qquad\qquad\qquad B_{x}=0+\mathrm l\Sigma M_{A}=0: \\ \\ \qquad -(15\mathrm{~kips})(3\mathrm{~ft})~+\,B_{y}(9\mathrm{~ft})-(6\mathrm{~kips})(11\mathrm{~ft})~-\mathrm{(6\ k i p s)}(13\,\mathrm{ft})=0 \\ \\ \qquad \qquad \qquad \qquad \qquad \qquad B_{y}=+21.0\mathrm{~kips}\qquad {\mathrm{B}}_{y}=21.0\mathrm{~kips}\uparrow
+\mathrm l\Sigma M_{B}=0: \\ \\ \qquad -A(9\mathrm{~ft})~+\,\mathrm{(15 ~kips)}(6\mathrm{~ft})-(6\mathrm{~kips})(2\mathrm{~ft})~-\mathrm{(6\ k i p s)}(4\,\mathrm{ft})=0 \\ \\ \qquad \qquad \qquad \qquad \qquad \qquad A=+6.00\mathrm{~kips}\qquad A=6.00\mathrm{~kips}\uparrow
Check. The results are checked by adding the vertical components of all of the external forces:
+\uparrow\Sigma F_{y}=\,+6.00\mathrm{~kips}\,-\,15\mathrm{~kips}\,+\,21.0\mathrm{~kips}\,-\,6\mathrm{~kips}\,-\,6\mathrm{~kips}\,=\,0Remark. In this problem the reactions at both A and B are vertical; however, these reactions are vertical for different reasons. At A, the beam is supported by a roller; hence the reaction cannot have any horizontal component. At B, the horizontal component of the reaction is zero because it must satisfy the equilibrium equation \Sigma F_{x}\,=\,0 and because none of the other forces acting on the beam has a horizontal component.
We could have noticed at first glance that the reaction at B was vertical and dispensed with the horizontal component {B}_{x}. This, however, is a bad practice. In following it, we would run the risk of forgetting the component {B}_{x} when the loading conditions require such a component (i.e., when a horizontal load is included). Also, the component {B}_{x} was found to be zero by using and solving an equilibrium equation, \Sigma F_{x}\, =\,0. By setting {B}_{x} equal to zero immediately, we might not realize that we actually make use of this equation and thus might lose track of the number of equations available for solving the problem.