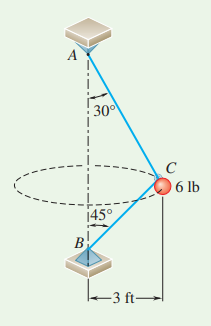
Question 12.SP.8: Two wires AC and BC are tied at C to a sphere that revolves ......
Two wires AC and BC are tied at C to a sphere that revolves at the constant speed v in the horizontal circle shown. Knowing that the wires will break if their tension exceeds 15 lb, determine the range of values of v for which both wires remain taut and the wires do not break.
Learn more on how we answer questions.
STRATEGY: You are given information about the forces in the wires, so use Newton’s second law. The sphere is moving along a curved path, so use normal and tangential coordinates.
MODELING: Choose the sphere for the system and assume you can treat it as a particle. Draw the free-body and kinetic diagrams as shown in Fig. 1. The tensions act in the direction of the wires, and the normal direction is toward the center of the circular path.
ANALYSIS: You can obtain scalar equations by applying Newton’s second law in the normal and vertical directions. Thus,
+←\Sigma F_{n}=m a_{n}\qquad T_{A C}\cos60^{\circ}+T_{B C}\cos45^{\circ}=m a_{n}=m{\frac{\nu^{2}}{\rho}} (1)
where m = W/g = 6 lb/(32.2 ft/s²) = 0.1863 lb·s²/ft and ρ = 3 ft. In these two equations, you have three unknowns, T_{AC},~T_{BC}, and v, so you need a third equation. The problem statement indicates that you want the range of speeds when both wires remain taut (that is, the tension is positive) and that this tension must be less than 15 lb. To find this range, first set each tension equal to zero and solve the resulting set of equations.
For T_{AC} = 0, you find v = 9.83 ft/s and T_{BC} = −8.485 lb, which is impossible for a wire.
For T_{BC}= 0, you find v = 7.468 ft/s and T_{AC} = 6.928 lb.
Thus, the minimum speed is 7.47 ft/s. Now set the tensions equal to 15 lb to find the maximum speed.
For T_{AC} = 15 lb, you find v = 15.29 ft/s and T_{BC} = 9.886 lb.
For T_{BC} = 15 lb, you find v = 18.03 ft/s and T_{AC} = 19.18 lb.
Therefore, the maximum speed is 15.29 ft/s. Combining these results gives you
7.47 ft/s ≤ v ≤ 15.29 ft/s ◂
REFLECT and THINK: In this problem, you needed to use the information in the problem statement to obtain additional equations so that you could determine the range of speeds. Another way to look at the solution is to solve Eqs. (1) and (2) for T_{AC}~and~T_{BC} in terms of v and to plot these as shown in Fig. 2. It is easy to see from this graph that T_{AC} determines the maximum speed and T_{BC} determines the minimum speed if both wires are to remain taut and also have tensions less than 15 lb.

