Question 8.SP.1: A 160-kN force is applied as shown at the end of a W200 × 52......

MODELING and ANALYSIS:
Shear and Bending Moment. Referring to Fig. 1, at section A–A′, we have

\begin{aligned} M_A & =(160  kN )(0.375  m )=60  kN \cdot m \\ V_A & =160  kN \end{aligned}

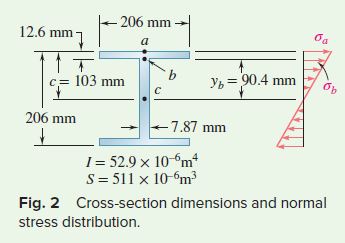
Normal Stresses on Transverse Plane. Referring to the table of Properties of Rolled-Steel Shapes in Appendix E to obtain the data shown, determine the stresses \sigma_a \text { and } \sigma_b (Fig. 2).

At point a,

\sigma_a=\frac{M_A}{S}=\frac{60  kN \cdot m }{511 \times 10^{-6}  m ^3}=117.4  MPa

At point b,

\sigma_b=\sigma_a \frac{y_b}{c}=(117.4  MPa ) \frac{90.4  mm }{103  mm }=103.0  MPa

Note that all normal stresses on the transverse plane are less than 150 MPa.

Shearing Stresses on Transverse Plane. Referring to Fig. 3, we obtain the data necessary to evaluate Q and then determine the stresses \tau_a and \tau_b .

At point a,

Q=0 \quad \tau_a=0

At point b,

\begin{aligned} & Q=(206 \times 12.6)(96.7)=251.0 \times 10^3  mm ^3=251.0 \times 10^{-6}  m ^3 \\ & \tau_b=\frac{V_A Q}{I t}=\frac{(160  kN )\left(251.0 \times 10^{-6}  m ^3\right)}{\left(52.9 \times 10^{-6}  m ^4\right)(0.00787  m )}=96.5  MPa \end{aligned}

Principal Stress at Point b. The state of stress at point b consists of the normal stress \sigma_b=103.0 MPa and the shearing stress \tau_b=96.5 MPa. Draw Mohr’s circle (Fig. 4) and find

\begin{aligned} \sigma_{\max } & =\frac{1}{2} \sigma_b+R=\frac{1}{2} \sigma_b+\sqrt{\left(\frac{1}{2} \sigma_b\right)^2+\tau_b^2} \\ & =\frac{103.0}{2}+\sqrt{\left(\frac{103.0}{2}\right)^2+(96.5)^2} \\ & =160.9  MPa \end{aligned}

\text { The specification, } \sigma_{\max } \leq 150  MPa \text {, is not satisfied. }

REFLECT and THINK: For this beam and loading, the principal stress at point b is 36% larger than the normal stress at point a. For L ≥ 881 mm (Fig. 5), the maximum normal stress would occur at point a.