Question 5.7: A 2000-hp, 2300-V, unity-power-factor, three-phase, Y-connec......
A 2000-hp, 2300-V, unity-power-factor, three-phase, Y-connected, 30-pole, 60-Hz synchronous motor has a synchronous reactance of 1.95 Ω/phase. For this problem all losses may be neglected.
a. Compute the maximum power and torque which this motor can deliver if it is supplied with power directly from a 60-Hz, 2300-V infinite bus. Assume its field excitation is maintained constant at the value which would result in unity power factor at rated load.
b. Instead of the infinite bus of part (a), suppose that the motor is supplied with power from a three-phase, Y-connected, 2300-V, 1500-kVA, two-pole, 3600 r/min turbine generator whose synchronous reactance is 2.65 Ω/phase. The generator is driven at rated speed, and the field excitations of generator and motor are adjusted so that the motor runs at unity power factor and rated terminal voltage at full load. Calculate the maximum power and torque which could be supplied corresponding to these values of field excitation.
Learn more on how do we answer questions.
Although this machine is undoubtedly of the salient-pole type, we will solve the problem by simple cylindrical-rotor theory. The solution accordingly neglects reluctance torque. The machine actually would develop a maximum torque somewhat greater than our computed value, as discussed in Section 5.7.
a. The equivalent circuit is shown in Fig. 5.14a and the phasor diagram at full load in Fig. 5.14b, where \hat{E}_{afm} is the generated voltage of the motor and X_{sm} is its synchronous reactance. From the motor rating with losses neglected,
\begin{aligned}\text{Rated kVA}& = 2000 × 0.746 = 1492 \text{kVA}, \text{three-phase}\\& = 497 \text{kVA}/\text{phase}\end{aligned}
\text{Rated voltage}= \frac{2300}{\sqrt{3}}=1328 V \text{line-to-neutral}
\text{Rated current}= \frac{497,000}{1328}= 374 V \text{A/phase-Y}
From the phasor diagram at full load
E_{afm}= \sqrt{V_a^2 +(I_aX_{sm})^2} = 1515 V
When the power source is an infinite bus and the field excitation is constant, V_a and E_{afm} are constant. Substitution of V_a \text{for} E_1, E_{afm} \text{for} E_2, \text{and} X_{sm} \text{for} X in Eq. 5.46 then gives
P_{1,max}=P_{2,max}=\frac{E_1E_2}{X} (5.46)
\begin{aligned}P_{max}&=\frac{V_aE_{afm}}{X_{sm}}=\frac{ 1328 × 1515}{1.95} =1032 kW/phase\\& = 3096 kW,\text{ three-phase}\end{aligned}
In per unit, P_{max} = 3096/1492 = 2.07 per unit. Because this power exceeds the motor rating, the motor cannot deliver this power for any extended period of time.
With 30 poles at 60 Hz, the synchronous angular velocity is found from Eq. 4.40
ω_s= \left(\frac{2}{\text{poles}}\right) ω_e (4.40)\\= \left(\frac{2}{30}\right) (2π60)=8π rad/sec
and hence
T_{max}=\frac{P_{max}}{ω_s}=\frac{3096 × 10^3}{8π} = 123.2 kN · m
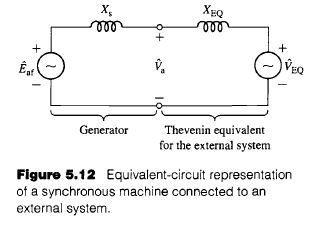
b. When the power source is the turbine generator, the equivalent circuit becomes that shown in Fig. 5.14c, where \hat{E}_{afg} is the generated voltage of the generator and X_{sg} is its synchronous reactance. Here the synchronous generator is equivalent to an external voltage \hat{V}_{EQ} and reactance X_{EQ} as in Fig. 5.12. The phasor diagram at full motor load, unity power factor, is shown in Fig. 5.14d. As before, V_a = 1330 V/phase at full load and E_{afm} = 1515 V/phase.
From the phasor diagram
E_{afg}=\sqrt{V_{ta}^ 2 + (I_aX_{sg})^2}= 1657 V
Since the field excitations and speeds of both machines are constant, E_{afg} \text{and} E_{afm} are constant. Substitution of E_{afg} \text{for} E_1, E_{afm} \text{for} E_2, \text{and} X_{sg} + X_{sm} \text{for} X in Eq. 5.46 then gives
\begin{aligned}P_{max}&=\frac{E_{afg}E_{afm}}{X_{sg} + X_{sm}}=\frac{1657 × 1515}{4.60} = 546 kW/phase \\&= 1638 kW, \text{three-phase}\end{aligned}
In per unit, P_{max} = 1638/1492 = 1.10 per unit.
T_{max}=\frac{P_{max}}{ω_s}=\frac{1635 × 10^3} {8π}= 65.2 kN · m
Synchronism would be lost if a load torque greater than this value were applied to the motor shaft. Of course, as in part (a), this loading exceeds the rating of the motor and could not be sustained under steady-state operating conditions.