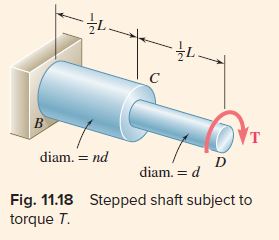
Question 11.CA.4: A circular shaft consists of two portions BC and CD of the s......
A circular shaft consists of two portions BC and CD of the same material and length, but of different cross sections (Fig. 11.18). Determine the strain energy of the shaft when it is subjected to a twisting couple T at end D. Express the results in terms of T, L, G, the polar moment of inertia J of the smaller cross section, and the ratio n of the two diameters.
Use Eq. (11.20) to compute the strain energy of each of the two portions of shaft, and add the expressions obtained. Note that the polar moment of inertia of portion BC is equal to n^4 J giving
U=\frac{T^2 L}{2 G J} (11.20)
U_n=\frac{T^2\left(\frac{1}{2} L\right)}{2 G J}+\frac{T^2\left(\frac{1}{2} L\right)}{2 G\left(n^4 J\right)}=\frac{T^2 L}{4 G J}\left(1+\frac{1}{n^4}\right)
or
U_n=\frac{1+n^4}{2 n^4} \frac{T^2 L}{2 G J} (1)
For n = 1,
U_1=\frac{T^2 L}{2 G J}
which is the expression given in Eq. (11.20) for a shaft of length L and uniform cross section. Note that, for n>1, U_n<U_1 . For example, when n = 2, U_2=\left(\frac{17}{32}\right) U_1 . Since the maximum shearing stress occurs in segment CD of the shaft and is proportional to the torque T, increasing the diameter of segment BC results in a decrease of the overall energy-absorbing capacity of the shaft.