Question 11.CA.14: A load P is supported at B by two rods of the same material ......
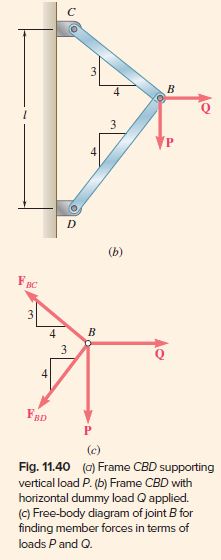
A load P is supported at B by two rods of the same material and the same cross-sectional area A (Fig. 11.40a). Determine the horizontal and vertical deflection of point B.
We apply a dummy horizontal load Q at B (Fig. 11.40b). From Castigliano’s theorem,
x_B=\frac{\partial U}{\partial Q} \quad y_B=\frac{\partial U}{\partial P}
Using Eq. (11.14) to obtain the strain energy for the rods
U=\frac{P^2 L}{2 A E} (11.14)
U=\frac{F_{B C}^2(B C)}{2 A E}+\frac{F_{B D}^2(B D)}{2 A E}
where F_{B C} \text { and } F_{B D} represent the forces in BC and BD, respectively. Therefore,
x_B=\frac{\partial U}{\partial Q}=\frac{F_{B C}(B C)}{A E} \frac{\partial F_{B C}}{\partial Q}+\frac{F_{B D}(B D)}{A E} \frac{\partial F_{B D}}{\partial Q} (1)
and
y_B=\frac{\partial U}{\partial P}=\frac{F_{B C}(B C)}{A E} \frac{\partial F_{B C}}{\partial P}+\frac{F_{B D}(B D)}{A E} \frac{\partial F_{B D}}{\partial P} (2)
From the free-body diagram of pin B (Fig. 11.40c),
F_{B C}=0.6 P+0.8 Q \quad F_{B D}=-0.8 P+0.6 Q (3)
Differentiating these equations with respect to Q and P, write
\frac{\partial F_{B C}}{\partial Q}=0.8 \quad \frac{\partial F_{B D}}{\partial Q}=0.6
\frac{\partial F_{B C}}{\partial P}=0.6 \quad \frac{\partial F_{B D}}{\partial P}=-0.8 (4)
Substituting from Eqs. (3) and (4) into both Eqs. (1) and (2), making Q = 0, and noting that BC = 0.6l and BD = 0.8l, the horizontal and vertical deflections of point B under the given load P are
\begin{aligned} x_B & =\frac{(0.6 P)(0.6 l)}{A E}(0.8)+\frac{(-0.8 P)(0.8 l)}{A E}(0.6) \\ & =-0.096 \frac{P l}{A E} \\ y_B & =\frac{(0.6 P)(0.6 l)}{A E}(0.6)+\frac{(-0.8 P)(0.8 l)}{A E}(-0.8) \\ & =+0.728 \frac{P l}{A E} \end{aligned}
Referring to the directions of the loads Q and P, we conclude that
x_B=0.096 \frac{P l}{A E} \leftarrow \quad y_B=0.728 \frac{P l}{A E} \downarrow
We check that the expression found for the vertical deflection of B is the same as obtained in Concept Application 11.9.
