Question 11.CSGP.179a: A refrigerator with R-12 as the working fluid has a minimum ......
A refrigerator with R-12 as the working fluid has a minimum temperature of −10°C and a maximum pressure of 1 MPa. Assume an ideal refrigeration cycle as in Fig. 11.21. Find the specific heat transfer from the cold space and that to the hot space, and the coefficient of performance.
Exit evaporator sat. vapor −10°C from B.3.1: h _1=183.19, \quad s _1=0.7019 \,kJ / kgK
Exit condenser sat. liquid 1 MPa from B.3.1: h _3=76.22\, kJ / kg
Compressor: s _2= s _1 \& P _2 \text { from B.3.2 } \Rightarrow h _2 \approx 210.1\, kJ / kg
Evaporator: q _{ L }= h _1- h _4= h _1- h _3=183.19-76.22= 1 0 7 \,k J / k g
Condenser: q _{ H }= h _2- h _3=210.1-76.22= 1 3 3 . 9\,k J / k g
COP: \beta= q _{ L } / w _{ c }= q _{ L } /\left( q _{ H }- q _{ L }\right)= 3 . 9 8
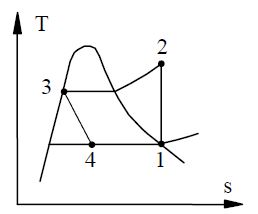
Ideal refrigeration cycle
\begin{aligned}& P _{\text {cond }}= P _3= P _2=1 \,MPa \\& T _{\text {evap }}=-10^{\circ} C = T _1\end{aligned}
Properties from Table B.3
