Question 8.15: A sodium-cooled fast reactor has the following characteristi......
A sodium-cooled fast reactor has the following characteristics:
P = 2400 MW(t) W = 14,000 kg/s
τ= 4.0 s c_p = 1,250 J/(kg °C)
M_ƒ c_ƒ = 13.5 × 10^6 J/°C M_c c_p = 1.90 × 10^6 J/°C
T_i = 360 °C
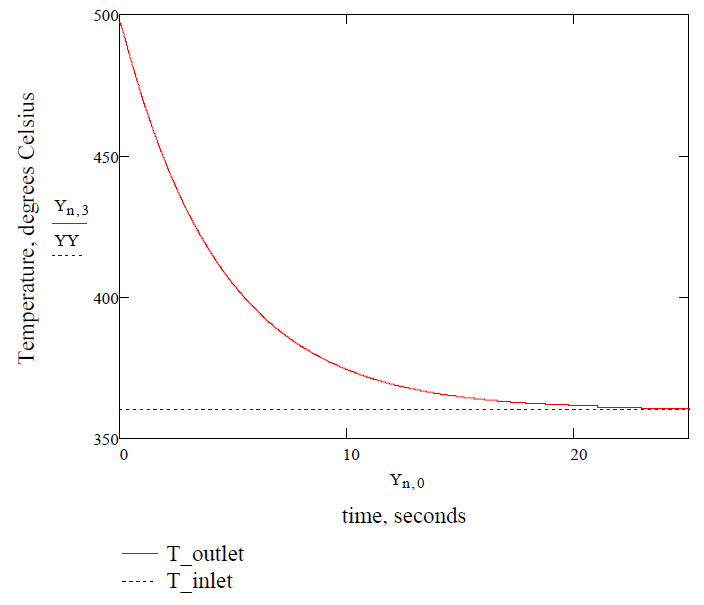
Suppose the reactor undergoes a sudden trip, which may be approximated by setting the power equal to zero. Assuming the inlet temperature remains at its initial value, find the core outlet temperature and plot your results.
Using equations [8.49] and [8.57], initial conditions y, and the stiff differential equation solver Radau (Mathcad), a vector Y was obtained. The first data column of Y after the time step column is the fuel temperature and the second column is average coolant temperature.
To find the core outlet temperature a third column needs to be added algebraically using the second column (average coolant temperature) and the inlet temperature (T_i)
\mathrm{R_{f}:=}\frac{\tau}{\mathrm{M_{fCf}}}=2.963\times10^{-7}
T_{\mathrm{c0}}:={\frac{ P}{2\cdot{ W\cdot c_p}}}+{T_i=428.571}
T_{\mathrm{f0}}:=\left({R}_{\mathrm{f}}+{\frac{1}{2 \cdot \textrm{W}\cdot{\mathrm{c_P}}}}\right)\cdot {P}+ {T}_{\mathrm{i}}=1.14\times10^{3}
{y}:={\left(\begin{array}{l}{{T}_{\mathrm{f0}}}\\ {{T}_{\mathrm{c0}}}\end{array}\right)}
D_1(t , y) := \begin {bmatrix}\frac{1}{\mathrm{M}_{\mathrm{fCf}}}.0-\frac{1}{\tau}\bigl({\bf y}_0-\mathrm{T}_{{i}}\bigr) \\ \Bigg[\frac{1}{\mathrm{R}_{\mathrm{f}}}.\mathrm{(y_0-y_1)}-2\cdot\mathrm{W.c}_{\mathrm{p}}.\mathrm{(y_1-T_{i})}\Bigg].\mathrm{\frac{1}{M_{\mathrm{ccp}}}}\end {bmatrix}
Y := radau (y , 0 , 100 , 10000 , D_1)
n := 0 , 1 .. 10000
YY := 360
{Y_{\mathrm{{n,3}}}:}=\left(2\cdot {Y_{\mathrm{{n,2}}}}\right)-{T_{\mathrm{{i}}}}
