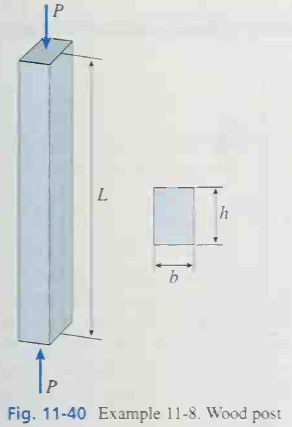
Question 11.8: A wood post of rectangular cross-section (Fig. 11-40) is con......

We will use the AFPA formulas (Eqs. 11-88a. b. and c) when analyzing this post. The critical Lid ratio (Eq. 11-89) is

σ_{allow}=F_c \quad \quad 0≤\frac{L}{d}≤11                 (11-88a)

σ_{allow}=F_c\left[1\ -\ \frac{1}{3}\left(\frac{L/d}{K_c}\right)^4\right] \quad \quad 11≤\frac{L}{d}≤K_c                 (11-88b)

σ_{allow}=\frac{0.3E}{(L/d)^2}=\frac{2F_c}{3}\left(\frac{K_c}{L/d}\right)^2\quad \quad K_c≤\frac{L}{d}≤50             (11-88c)

K_c=\sqrt{\frac{0.45E}{F_c}}=\sqrt{\frac{0.45(14\ GPa)}{15\ MPa}} = 20.5

Since buckling may occur in any direction, the actual L/d ratio is

\frac{L}{d}=\frac{L}{0.120\ m}

in which L has units of meters and d is the least dimension of the cross section, that is. d = b.
(a) Allowable axial load. Since the length L = 1.8 m. the L/d ratio is

\frac{L}{d}=\frac{1.8\ m}{0.120\ m} = 15

which is between 11 and K_c. Therefore, we use Eq. ( 11-88b) to obtain the allowable stress:

σ_{allow}=F_c\left[1\ -\ \frac{1}{3}\left(\frac{L/d}{K_c}\right)^4\right]=(15\ MPa)\left[1\ -\ \frac{1}{3}\left(\frac{15}{20.5}\right)^4\right] = 13.6 MPa

Knowing the allowable stress, we can now calculate the allowable axial load:

P_{allow}=σ_{allow}A=σ_{allow}bh = (13.6 MPa)(120 mm × 160 mm) = 261 kN

(b) Maximum allowable length. Since the length of the column is unknown at this stage, we do not know the L/d ratio. Therefore, we do not know which formula to use for the allowable stress. As a trial, we will use Eq. (11-88c), for which Lid is between K_c and 50:

σ_{allow}=\frac{0.3E}{(L/d)^2}=\frac{0.3(14\ GPa)}{(L/d)^2}=\frac{4200\ MPa}{(L/d)^2}

Now we replace σ_{allow} by the actual stress P/A, which is

\frac{P}{A}=\frac{140\ kN}{(120\ mm)(160\ mm)} = 7.29 MPa

and obtain

7.29 MPa=\frac{4200\ MPa}{(L/d)^2}

Thus. the L/d ratio is

\frac{L}{d} = 24

which is between K_c and 50, as assumed. Therefore, the maximum allowable length is

L_{max} = 24d = 24(120 mm) = 2.88 m