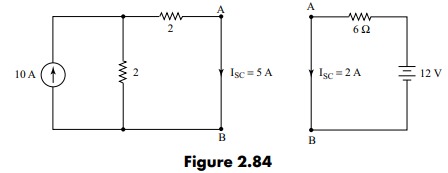
Question 2.30: Apply Norton’s theorem to determine the current flowing thro......
Apply Norton’s theorem to determine the current flowing through the resistance of 6 Ω connected across the terminals. A and B. Also calculate the potential of point A. What will be the current through the 6 Ω resistor across AK. Solve this problem using Thevenin’s theorem also.
After removing the 6 Ω resistor across terminals A and B, we short circuit the terminals and determine I_{sc} due to the current source and also due to the voltage source and then add them to find their combined effect. Terminals A and B have been shown short circuited separately for each of the voltage sources.
Total \mathrm{I}_{\mathrm{sc}}=5+2=7 \mathrm{~A}
Equivalent resistance across A and B is determined by open circuiting the current source and short circuiting the voltage source.
\mathrm{R}_{\mathrm{eq}}=\mathrm{R}_{\mathrm{AB}}=\frac{6 \times 4}{6+4}=2.4 \OmegaNorton’s equivalent circuit is shown in Fig. 2.86. Using the current divider rule current, I is calculated as
I=\frac{7 \times 2.4}{2.4+6}=2 \mathrm{~A}The potential of A with respect to B = 6 × 2 = 12 V
Since potential across A and B is 12 V and the potential of point K with respect to point B is again 12 V, no current will flow through the resistor connected between terminals A and K.
Now, let us apply Thevenin’s theorem
We convert the current source into its equivalent voltage source of the network and redraw it as
Remove the 6 Ω resistor across AB and determine V_{OC},
We write,
+20 \mathrm{~V}-2 \mathrm{I}-2 \mathrm{I}-6 \mathrm{I}-12 \mathrm{~V}=0or, 10 I = 8 V
I = 0.8 A
\mathrm{V}_{\mathrm{OC}}=+12+6 \times 0.8=16.8 \mathrm{~V}.
R_{eq} across AB after short circuiting the source of EMFs, R_{e q}=R_{A B}=\frac{6 \times 4}{6+4}=2.4 \Omega
Thevenin’s equivalent circuit is
I=\frac{16.8}{R_{\mathrm{Th}}+R}=\frac{16.8}{2.4+6}=2 \mathrm{~A}
