Question 28.9: Beta decay in our bodies The body normally contains about 7 ......
Beta decay in our bodies
The body normally contains about 7 mg of radioactive potassium -40{ }_{19}^{40} \mathrm{~K} . It is present in some of the foods we eat (e.g., bananas). Each second, about 2 × 10³ of these potassium nuclei undergo either beta-plus or beta-minus decay. Assume that all decays are beta-plus and that 40% of the energy released is absorbed by the body (the percent depends on the ratio of beta-minus decay to beta-plus decay, body thickness, the energy of the neutrinos produced in the decays, and other factors). Determine the energy in MeV transferred to the body each second by { }_{19}^{40} \mathrm{~K} beta-plus decay. What is the rate of energy transfer in watts?
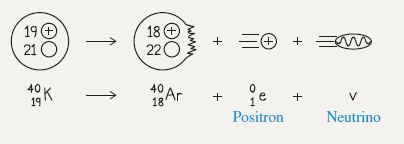
Sketch and translate A single beta-plus decay is sketched below. If we determine the energy released by a single decay, we can then determine the rate of energy transfer to the body.
Simplify and diagram The system of interest will be the potassium atom and its decay products.
Represent mathematically The Q of a single beta plus decay is
Q=\left[m\left({ }_{19}^{40} \mathrm{~K}\right)-m\left({ }_{18}^{40} \mathrm{Ar}\right)-m\left({ }_1^0 e\right)\right] c^2
The rate of energy transferred to the body (ΔU>Δt) will be
40% of Q times the number (ΔN>Δt) of decays per second,
or
\frac{\Delta U}{\Delta t}=\frac{\Delta N}{\Delta t}(0.4 Q)
Learn more on how do we answer questions.
Solve and evaluate From the appendix of selected isotopes we find the masses of the atoms in atomic mass units (u):
Q=\left(39.964000 \mathrm{u}-39.962384 \mathrm{u}-5.4858 \times 10^{-4} \mathrm{u}\right) c^2
=(0.001068 \mathrm{u}) c^2\left(\frac{931.5 \mathrm{MeV}}{\mathrm{u} \cdot c^2}\right)
= 0.995 MeV
The energy transferred to the body per second is then
\frac{\Delta U}{\Delta t}=(2000 \text { decays } / \mathrm{s})(0.995 \mathrm{MeV})(0.4)=800 \mathrm{MeV} / \mathrm{s}In watts this is
\frac{\Delta U}{\Delta t}=(800 \mathrm{MeV} / \mathrm{s})\left(\frac{1.6 \times 10^{-13} \mathrm{~J}}{\mathrm{MeV}}\right)
=1.3 \times 10^{-10} \mathrm{~W}
\approx 1 \times 10^{-10} \mathrm{~W}
This is extremely small compared to the average human metabolic rate of 100 W. We’ll see in a later section whether these beta particles cause any negative health effects.
Try it yourself: Is more or less energy released by potassium- 40 beta-minus decay than beta-plus decay?
Answer: The product of the beta-minus decay is { }_{20}^{40} \mathrm{Ca} , which has mass 39.962591 u. This is slightly greater than the 39.962383-u { }_{18}^{40} \mathrm{Ar} product mass of the beta-plus decay. The beta-plus decay releases more energy.