Question 1.13: Determine the currents in various elements of the bridge cir......
Determine the currents in various elements of the bridge circuit shown in Fig. 1, using mesh analysis.

Learn more on how do we answer questions.
The graph of the given circuit is shown in Fig. 2. It has 6 branches and 4 nodes. Hence, the number of meshes m in the circuit is,
m = B – N + 1 = 6 – 4 + 1 = 3.
The circuit has 6 currents (corresponding to six branches) and in this 3 currents are independent (corresponding to three meshes).
Let us assume three mesh currents as shown in Fig. 2. The direction of the current are chosen arbitrarily. The circuit with chosen mesh currents is shown in Fig. 3.
Method I : Formation of mesh basis equation by applying KVL
In this method, the mesh equations are formed using Kirchhoff’s Voltage Law.
The mesh equation for a mesh is formed by equating the sum of voltage fall to the sum of voltage rise.
The voltage rise and fall are determined by tracing the circuit in the direction of the mesh current. With reference to Fig. 4, the mesh equation for mesh-1 is formed as shown below:
\text { Voltage fall: } I _1, I _1, I _1 \\ \text { Voltage rise: } I _2, I _3, 5 \\\qquad \therefore I _1+ I _1+ I _1= I _2+ I _3+5 \\ \quad 3 I _1- I _2- I _3=5 …..(1)
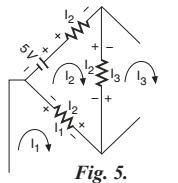
With reference to Fig. 5, the mesh equation for mesh-2 is formed as shown below:
\text { Voltage fall : } I_2, I_2, I_2 \\\text { Voltage rise: } I_1, I_3, 5 \\ \therefore \quad I_2+I_2+I_2=I_1+I_3+5 \\ \quad-I_1+3 I_2-I_3=5 …..(2)
With reference to Fig. 6, the mesh equation for mesh-3 is formed as shown below:
\text { Voltage fall : } I_3, I_3, I_3 \\\text { Voltage rise: } I_1, I_2, I_{10} \\ \therefore \quad I_3+I_3+I_3=I_1+I_2+10 \\ \quad-I_1-I_2+3I_3=10 …..(3)
Equations (1), (2) and (3) are the mesh equations of the circuit shown in Fig. 3. The mesh equations are summarised here for convenience.
3 I_1-I_2-I_3=5 \\ -I_1+3 I_2-I_3=5 \\ -I_1-I_2+3 I_3=10The mesh equations can be arranged in the matrix form as shown below and then solved by Cramer’s rule.
\left[\begin{array}{rrr}3 & -1 & -1 \\-1 & 3 & -1 \\-1 & -1 & 3\end{array}\right]\left[\begin{array}{l}I_1 \\I_2\\I_3\end{array}\right]=\left[\begin{array}{r} 5 \\ 5 \\10\end{array}\right] …..(4)
Method II : Formation of mesh basis equation by inspection
In this method, the mesh basis matrix equation is formed directly from the circuit shown in Fig.3 by inspection. The circuit has three meshes. The general form of mesh basis matrix equation for three mesh circuit is shown in equation (5).
\left[\begin{array}{lll} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33}\end{array}\right]\left[\begin{array}{l} I_1 \\ I_2 \\ I_3\end{array}\right]=\left[\begin{array}{l} E_{11} \\ E_{22} \\ E_{33}\end{array}\right] …..(5)
The elements of the resistance matrix and source voltage matrix are formed as shown below:
On substituting the above terms in equation (5), we get,
\left[\begin{array}{rrr} 3 & -1 & -1 \\ -1 & 3 & -1 \\ -1 & -1 &3\end{array}\right]\left[\begin{array}{l} I_1 \\ I_2 \\ I_3 \end{array}\right]=\left[\begin{array}{r} 5 \\ 5 \\ 10 \end{array}\right] ….. (6)
Solution of mesh currents
It is observed that the mesh basis matrix equation obtained in method I and II are the same. In equation (6) the unknowns are I _1, I _2 \text { and } I _3 . In order to solve I _1, I _2 \text { and } I _3, let us define four determinants ∆, ∆_1 , ∆_2 and ∆_3 as shown below:
The determinants are evaluated by expanding along first row and the mesh currents are solved by Cramer’s rule.
\Delta=\left|\begin{array}{rrr} 3 & -1 & -1 \\ -1 & 3 & -1 \\ -1 & -1 & 3 \end{array}\right|=3 \times[3 \times 3-(-1) \times(-1)]-(-1) \times[-1 \times 3-(-1) \times(-1)] +(-1)\times[-1\times(-1)-(-1)\times 3]\\=24-4-4=16
\Delta_1=\left|\begin{array}{rrr} 5 & -1 & -1 \\ 5 & 3 & -1 \\ 10 & -1 & 3 \end{array}\right|=5 \times[3 \times 3-(-1) \times(-1)]-(-1) \times[5 \times 3-10 \times(-1)]+(-1) \times[5 \times(-1)-10 \times 3] \\=40+25+35=100
\Delta_2=\left|\begin{array}{rrr} 3 & 5 & -1 \\-1 & 5 & -1 \\ -1 & 10 & 3\end{array}\right|=3 \times[5 \times 3-10 \times(-1)]-5 \times[-1 \times 3-(-1) \times(-1)]+(-1) \times[-1 \times 10-(-1) \times 5] \\ =75+20+5=100
\Delta_3=\left|\begin{array}{rrr} 3 & -1 & 5 \\ -1 & 3 & 5 \\ -1 & -1 & 10 \end{array}\right|=3 \times[3 \times 10-(-1) \times 5]-(-1) \times[-1 \times 10-(-1) \times 5]+5 \times[-1 \times(-1)-(-1) \times 3] \\ =105-5+20=120
I_1=\frac{\Delta_1}{\Delta}=\frac{100}{16}=6.25 A \\I_2=\frac{\Delta_2}{\Delta}=\frac{100}{16}=6.25 A \\ I_3=\frac{\Delta_3}{\Delta}=\frac{120}{16}=7.5 AThe relation between mesh and branch currents can be obtained from Fig. 3 and branch currents are evaluated as shown below:
I_{ a }= I _1=6.25 A \\I_{ b }= I_2=6.25 A \\I_{ c }= I _1- I _2=6.25-6.25=0 \\I_{ d }= I _3=7.5 A \\I_e= I_1- I_3=6.25-7.5=-1.25 A \\I_{ f }= I _2- I _3=6.25-7.5=-1.25 A